Một lăng kính thuỷ tinh có chiết suất n = 1,5, tiết diện là một tam giác đều, được đặt trong không khí. Chiếu tia sáng SI tới mặt bên của lăng kính với góc tới i = 300. Góc lệch của tia sáng khi đi qua lăng kính là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
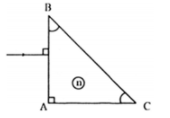
Báo saiLăng kính tam giác đều nên góc chiết quang A = 600.
Định luật khúc xạ ánh sáng tại I:
\(\sin {{i}_{1}}=n\sin {{r}_{1}}\Rightarrow \sin {{r}_{1}}=\frac{\sin {{i}_{1}}}{n}=\frac{\sin {{30}^{0}}}{1,5}=\frac{1}{3}.\)
\(\Rightarrow {{r}_{1}}=\arcsin \left( \frac{1}{3} \right)={{19}^{0}}28'.\)
Ta có:
\(A={{r}_{1}}+{{r}_{2}}\Rightarrow {{r}_{2}}=A-{{r}_{1}}={{60}^{0}}-{{19}^{0}}28'=40{}^{0}32'.\)
Định luật khúc xạ ánh sáng tại J:
\(\sin {{i}_{2}}=n\sin {{r}_{2}}=1,5.\sin {{40}^{0}}32'=0,975.\)
\(\Rightarrow {{i}_{2}}=\arcsin \left( 0,975 \right)={{77}^{0}}10'.\)
Góc lệch \(D=r-i={{77}^{0}}10-{{30}^{0}}={{47}^{0}}10'.D=r-i={{77}^{0}}10-{{30}^{0}}={{47}^{0}}10'.\)
Câu hỏi liên quan
-
Chiếu một tia sáng dưới một góc tới 250 vào một lăng kính đặt trong không khí có có góc chiết quang 500 và chiết suất 1,4. Góc lệch của tia sáng qua lăng kính là:
-
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phản xạ toàn phần trên hai mặt AC và AB, tia ló ra khỏi đáy BC theo phương vuông góc với BC. Tính góc chiết quang A:
-
Có ba trường hợp truyền tia sáng qua lăng kính như hình vẽ. Ở các trường hợp nào sau đây, lăng kính không làm tia ló lệch về phía đáy?
-
Một tia sáng từ không khí đến gặp một lăng kính có góc chiết quang A = 600, chiết suất \(n=\sqrt{3}\) dưới góc tới \(i={{60}^{0}}.\) Khi tăng góc tới một ít thì góc lệch như thế nào?
-
Phát biểu nào sau đây là đúng?
-
Chiếu một tia sáng đến lăng kính thì thấy tia ló ra là một tia sáng đơn sắc. Có thể kết luận tia sáng chiếu tới lăng kính là ánh sáng:
-
Chiếu một chùm sáng song song tới mặt bên của một lăng kính và có tia ló ra mặt bên còn lại. Khi thay đổi góc tới của tia tới thì góc lệch giữa tia ló so với tia tới
-
Lăng kính là:
-
Chiếu một chùm sáng đến lăng kính thì thấy tia ló ra là chùm ánh sáng nhiều màu sắc khác nhau từ đỏ đến tím. Có thể kết luận chùm sáng chiếu tới lăng kính là ánh sáng:
-
Một lăng kính thủy tinh có chiết xuất n = 1,5. Chiếu một tia sáng qua lăng kính, để góc lệch cực tiểu bằng góc chiết quang A thì góc chiết quang A phải bằng
-
Khi xảy ra góc lệch cực tiểu nếu giảm góc tới i một vài độ thì góc lệch sẽ
-
Sử dụng hình vẽ về đường đi của tia sáng qua lăng kính: SI là tia tới, JR là tia ló, D là góc lệch giữa tia tới và tia ló, n là chiết suất của chất làm lăng kính. Công thức nào trong các công thức sau đây là đúng?
-
Tiêu cự của thấu kính được tính bởi công thức
-
Công thức xác định góc lệch D của tia sáng qua lăng kính là
-
Lăng kính có góc chiết quang A và chiết suất \(n=\sqrt{2}.\) Khi ở trong không khí thì góc lệch có giá trị cực tiểu Dmin = A. Góc chiết quang của A bằng
-
Tia tới vuông góc với mặt bên của lăng kính thuỷ tinh có chiết suất n = 1,5 góc chiết quang A. Tia ló hợp với tia tới một góc lệch D = 300. Góc chiết quang của lăng kính là
-
Chiếu một tia sáng đơn sắc đến mặt bên AB của một lăng kính tiết diện là một tam giác đều ABC theo phương song song với đáy BC. Tia ló ra khỏi AC đi là là mặt AC. Chiết suất của chất làm lăng kính là:
-
Chọn câu sai. Chiếu một chùm tia sáng vào một mặt bên của lăng kính ở trong không khí thì
-
Phát biểu nào sau đây là đúng?
-
Lăng kính được cấu tạo bằng khối chất trong suốt, đồng chất, thường có dạng hình lăng trụ. Tiết diện thẳng của lăng kính hình
