Một con lắc lò xo dao động điều hòa theo phương ngang với tần số góc \(\omega \). Vật nhỏ của con lắc có khối lượng 100g. Tại thời điểm t=0, vật nhỏ qua vị trí cân bằng theo chiều dương. Tại thời điểm t=0,95s, vận tốc v và li độ x của vật nhỏ thỏa mãn \(v=-\omega x\)à thứ 5. Lấy \({\pi ^2} = 10\). Độ cứng của lò xo là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐể tính được độ cứng của lò xo, ta cần tính được \(\omega\) , hay tính được chu kì của vật.
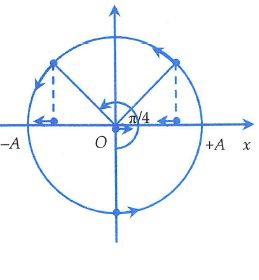
Khi \(v=-\omega x\) ta có \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {x^2} + {x^2}\) , suy ra \(x = \pm \frac{A}{{\sqrt 2 }}\) . Vậy, khi \(v=-\omega x\) thì vật đi qua vị trí có li độ \(x = \frac{A}{{\sqrt 2 }}\)theo chiều âm, hoặc qua vị trí có li độ \(x =-\frac{A}{{\sqrt 2 }}\)theo chiều dương.
Từ đó suy ra: 1 chu kì sẽ có hai lần vận tốc và li độ thỏa mãn \(v=-\omega x\), dựa vào đường tròn suy ra .\(0,95 = 2T + \frac{T}{4} + \frac{T}{8} \Rightarrow T = - 0,4s\)
Độ cứng của lò xo .\(k = \frac{{4{\pi ^2}m}}{{{T^2}}} = 25N/m\)