Cho mạch điện (như hình vẽ).
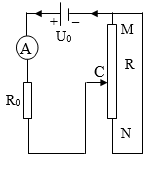
Biết Uo = 12 V, Ro là điện trở, R là biến trở ampe kế lí tưởng. Khi con chạy C của biến trở R từ M đến N, ta thấy ampe kế chỉ giá trị lớn nhất I1 = 2A. Và giá trị nhỏ nhất I2 = 1A. Bỏ qua điện trở của các dây nối. Xác định giá trị Ro và R lần lượt là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiVới mạch điện này thì: RMC // RNC và RMC + RNC = R
Vì vậy khi ta đặt RMC = x (Ω) ⇒ RNC = R – x (0 < x < R)
\( \Rightarrow {R_{MNC}} = \frac{{x(R - x)}}{R}\)
Khi đó chỉ số của am pe kế là:
\(I = \frac{{{U_o}}}{{{R_o} + {R_{MNC}}}} = \frac{{{U_o}}}{{{R_o} + \frac{{x(R - x)}}{R}}}\)
+) Khi con chạy C ở M (ở N) thì RMNC = 0 và lúc đó ampe kế sẽ chỉ giá trị cực đại:
\({I_{\max }} = \frac{{{U_o}}}{{{R_o}}} \Rightarrow {R_o} = \frac{{{U_o}}}{{{I_{\max }}}} = \frac{{12}}{2} = 6\Omega \)
+) Để am pe kế chỉ giá trị nhỏ nhất thì:
\({R_{CNM}} = \frac{{x(R - x)}}{R}\) phải có giá trị cực đại, ta triển khai RCNM
\({R_{CNM}} = \frac{{x(R - x)}}{R} = \frac{{ - {x^2} + Rx}}{R} = \frac{{ - {x^2} + Rx - \frac{{{R^2}}}{4} + \frac{{{R^2}}}{4}}}{R} = \frac{{\frac{{{R^2}}}{4} - {{\left( {x - \frac{R}{2}} \right)}^2}}}{R} \le \frac{R}{4}\)
Để RMNC có giá trị cực đại bằng R/4 thì:
\({\left( {x - \frac{R}{2}} \right)^2} = 0 \Leftrightarrow x = \frac{R}{2}\Omega \)
Tức là con chạy C ở chính giữa của biến trở và
\(\begin{array}{l} \Rightarrow {R_{CNM}} = \frac{R}{4}\Omega \Rightarrow {I_{\min }} = \frac{{{U_o}}}{{{R_o} + \frac{R}{4}}} = 1\\ \Leftrightarrow \frac{{12}}{{6 + \frac{R}{4}}} = 1 \Rightarrow R = 24\Omega \end{array}\)
Câu hỏi liên quan
-
Một cái ấm bằng nhôm có khối lượng 0,3kg chứa 2lít nước ở 200C. Muốn đun sôi ấm nước này cần nhiệt lượng bao nhiêu? Biết nhiệt dung riêng của nhôm và của nước lần lượt là: 880J/kg.k và 4200J/kg.k
-
Một bóng đèn có hiệu điện thế định mức 2,5V và cường độ dòng điện định mức 0,4A được mắc với một biến trở con chạy để sử dụng với nguồn điện có hiệu điện thế không đổi 12V. Đèn và biến trở phải mắc với nhau như thế nào để đèn có thể sáng bình thường?
-
Mạch điện có sơ đồ như hình vẽ. Trong đó R1 = 12, R2 = R3 = 6 Ω; UAB = 12v; RA ≈; Rv rất lớn.
.png)
Tính số chỉ của ampe kế, vôn kế và công suất thiêu thụ điện của đoạn mạch AB.
-
Bóng đèn có điện trở \(9\Omega\) và hiệu điện thế qua nó là 24V thì nó sáng bình thường. Tính công suất định mức của bóng đèn?
-
Cho các dụng cụ sau: một nguồn điện có hiệu điện thế không đổi U = 12 V hai bóng đèn Đ1 (6 V - 0,4 A); Đ2 (6V - 0,1A) và một biến trở Rb. Tính công suất tiêu thụ của biến trở ứng với mỗi sơ đồ.
-
Khi mắc một bóng đèn có hiệu điện thế 220V thì dòng điện chạy qua nó có cường độ 455mA. Tính điện trở và công suất của bóng điện khi đó.
-
Trong công thức P = I2.R Nếu tăng gấp đôi điện trở R và giảm cường độ dòng điện 4 lần thì công suất:
-
Cho mạch điện như hình vẽ (Hình 3). UAB = 90V; R1 = 40 Ω; R2 = 90Ω; R4 = 20Ω; R3 là một biến trở. Bỏ qua điện trở của ampe kế, dây nối và khoá K.
.png)
Khi mở khóa K và điều chỉnh cho R3 = 30Ω. Tính số chỉ của ampe kế.
-
Trên bóng đèn Đ1, Đ2 có ghi số tương ứng là 3V - 1,2W và 6V - 6W. Cần mắc hai đèn này cùng với một biến trở vào hiệu hiệu điện thế U = 9V để hai đèn sáng bình thường. Cần ắmc hai đèn và biến trở như thế nào để thỏa mãn yêu cầu của đề bài?
-
Khi có dòng điện I1=1A đi qua một dây dẫn trong một khoảng thời gian thì dây đó nóng lên đến nhiệt độ t1=40°C. Khi có dòng điện I2= 2A đi qua thì dây đó nóng lên đến nhiệt độ t2=100°C. Hỏi khi có dòng điện I3=4A đi qua thì nó nóng lên đến nhiệt độ t3 bằng bao nhiêu? Coi nhiệt độ môi trường xung quanh và điện trở dây dẫn là không đổi. Nhiệt lượng toả ra ở môi trường xung quanh tỷ lệ thuận với độ chênh nhiệt độ giữa dây dẫn và môi trường xung quanh.
-
Từ công thức tính công suất hao phí, đề giảm hao phí khi truyền tải điện năng đi xa, ta chọn phương án nào trong các phương án sau:
-
Một ấm điện có hai dây dẫn R1 và R2 để đun nước. Nếu dùng dây R1 thì nước trong ấm sẽ sôi sau thời gian t1 = 10 (phút). Còn nếu dùng dây R2 thì nước sẽ sôi sau thời gian t2 = 40 (phút). Nếu dùng cả hai dây mắc song song thì nước sẽ sôi sau thời gian là:
-
Công thức nào sau đây không đúng?
-
Một bếp điện có điện trở R được mắc vào hiệu điện thế U thì dòng điện qua nó có cường độ I. Khi đó công suất của bếp là P. Biểu thức nào sau đây xác định P không đúng?
-
Công thức nào sau đây không phải là công thức tính công của dòng điện?
-
rên bóng đèn dây tóc Đ1 có ghi 220V – 100W. Trên bóng đèn dây tóc Đ2 có ghi 220V – 75W. Mắc hai bóng đèn nối tiếp với nhau rồi mắc đoạn mạch này vào hiệu điện thế 220V. Tính công suất điện của đoạn mạch nối tiếp này, cho rằng điện trở của mỗi đèn khi đó bằng 50% điện trở của đèn đó khi sáng bình thường.
-
Một bàn là ghi 220V - 1000W. Tính điện trở và cường độ dòng điện định mức của bàn là
-
Đơn vị của công suất điện là:
-
Cho hai đèn Đ1 (3V - 3W); Đ2 (6V - 6W) mắc nối tiếp với nhau vào hiệu điện thế 18V. Xác định các giá trị định mức của bóng đèn?
-
Điện trở của bếp điện làm bằng nikelin R = 48,5 Ω. Bếp được sử dụng ở hiệu điện thế U = 220V. Công suất tiêu thụ của bếp điện gần đúng nhất là bao nhiêu?
