Cho hình bình hành ABCD. Gọi Ax, By,Cz,Dt lần lượt là các đường thẳng song song với nhau đi qua A,B,C,D và nằm về cùng một phía của mp(ABCD), đồng thời không nằm trong mp(ABCD). Một mặt phẳng (P) lần lượt cắt Ax, By, Cz, Dt lần lượt tại A’,B’,C’,D’ biết AA’ = x,BB’ = y, CC’ = z. Khi đó DD’ bằng:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai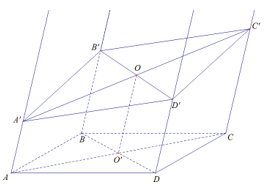
Trên Ax lấy điểm A’ sao cho AA’ = x
Trên By lấy điểm B’ sao cho BB’ = y
Trên Cz lấy điểm C’ sao cho CC’ = z
Gọi (α) là mặt phẳng chứa tia Cz và Dt
Xét (A’B’C’) và (α) có:
C’ là điểm chung
A’B’ // (α)
⇒ giao tuyến của (α) và (A’B’D’) là đường thẳng d đi qua C’ và song song với A’B’
Trong mặt phẳng (α), ta có: d cắt Dt tại D’
Gọi {O} = AC ∩ BD,{O'} = AC' ∩ B'D'
Xét hình thang AA’C’C có: OO’ là đường trung bình
\( \Rightarrow OO' = \frac{{AA' + CC'}}{2} = \frac{{x + z}}{2}\)
Xét tam giác BDD’D có: OO’ là đường trung bình
\( \Rightarrow OO' = \frac{{DD' + BB'}}{2} \Rightarrow DD' = x + z - y\)














