Trắc nghiệm Đại cương về đường thẳng và mặt phẳng Toán Lớp 11
-
Câu 1:
Tìm tọa độ điểm đối xứng của M(22;−15;7) qua gốc tọa độ O.
A. (22; 15; 7)
B. (22; -15; -7)
C. (-22; 15; 7)
D. (-22; 15; -7)
-
Câu 2:
Trong không gian Oxyz, cho hai điểm A(4;0;4) và B(2;4;0). Điểm M di động trên tia Oz, điểm N di động trên tia Oy. Đường gấp khúc AMNB có độ dài nhỏ nhất bằng bao nhiêu? (Kết quả làm tròn đến hàng phần chục).
A. 10,1
B. 11,3
C. 9,9
D. 10,0
-
Câu 3:
Cho năm điểm A, B, C, D, E sao cho không có bốn điểm nào cùng nằm trên một mặt phẳng. Số hình tứ diện có các đỉnh lấy từ năm điểm đã cho là
A. 5
B. 4
C. 3
D. 2
-
Câu 4:
Cho hình chóp (S.ABCD )có đáy (ABCD ) là hình thang (( (AB//CD) ) ). Gọi (I,J ) lần lượt là trung điểm của các cạnh (AD, ,BC )và G là trọng tâm tam giác (SAB ). Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sao đây đúng?
A. AB=13CD
B. AB=32CD
C. AB=3CD
D. AB=23CD
-
Câu 5:
Cho hình bình hành (ABCD ). Qua (A ), (B ), (C ), (D ) lần lượt vẽ các nửa đường thẳng Ax, By, Cz, Dt ở cùng phía so với mặt phẳng (ABCD), song song với nhau và không nằm trong (( (ABCD) ) ). Một mặt phẳng (P) cắt Ax, By, Cz, Dt tương ứng tại (A' ), (B' ), (C' ), (D' ) sao cho AA' = 3, BB' = 5, CC' = 4. Tính DD'.
A. 4
B. 6
C. 2
D. 12
-
Câu 6:
Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB//CD) . Khẳng định nào sau đây sai?
A. Hình chóp S.ABCD có 4 mặt bên
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO (O là giao điểm của AC và BD).
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI (I là giao điểm của AD và BC)
D. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABCD.
-
Câu 7:
Trong các khẳng định sau, khẳng định nào đúng?
A. Nếu 3 điểm A,B,C là 3 điểm chung của 2 mặt phẳng (P) và (Q) thì A,B,C thẳng hàng..
B. Nếu A,B,C thẳng hàng và (P), (Q) có điểm chung là A thì B,C cũng là 2 điểm chung của (P) và (Q)..
C. Nếu 3 điểm A,B,C là 3 điểm chung của 2 mặt phẳng (P)và (Q) phân biệt thì A,B,C không thẳng hàng..
D. Nếu A,B,C thẳng hàng và A,B là 2 điểm chung của (P) và (Q) thì C cũng là điểm chung của (P) và (Q).
-
Câu 8:
Chọn khẳng định sai trong các khẳng định sau?
A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa
B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất
C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất
D. Nếu ba điểm phân biệt M,N,P cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.
-
Câu 9:
Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu?
A. 3
B. 4
C. 5
D. 6
-
Câu 10:
Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là :
A. 5 mặt, 5 cạnh
B. 6 mặt, 5 cạnh
C. 6 mặt, 10 cạnh
D. 5 mặt, 10 cạnh
-
Câu 11:
Trong các hình sau: Các hình có thể là hình biểu diễn của một hình tứ diện là:
A. (I)
B. (I),(II),(III)
C. (I),(II),(IV)
D. (I),(II),(III),(IV)
-
Câu 12:
Cho năm điểm A,B,C,D,E trong đó không có bốn điểm nào ở trên cùng một mặt phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi ba trong số năm điểm đã cho?
A. 10
B. 12
C. 14
D. 16
-
Câu 13:
Cho tứ giác ABCD. Có thể xác định được bao nhiêu mặt phẳng chứa tất cả các đỉnh của tứ giác ABCD
A. 1
B. 2
C. 3
D. 0
-
Câu 14:
Trong mp (α), cho bốn điểm A,B,C,D trong đó không có ba điểm nào thẳng hàng. Điểm (S notin mp (α) ). Có mấy mặt phẳng tạo bởi S và hai trong số bốn điểm nói trên?
A. 4
B. 5
C. 6
D. 7
-
Câu 15:
Trong các khẳng định sau, khẳng định nào đúng?
A. Qua 2 điểm phân biệt có duy nhất một mặt phẳng..
B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng..
C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng..
D. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng..
-
Câu 16:
Cho bốn điểm không đồng phẳng, ta có thể xác định được nhiều nhất bao nhiêu mặt phẳng phân biệt từ bốn điểm đã cho ?
A. 2
B. 3
C. 4
D. 6
-
Câu 17:
Cho tứ giác lồi ABCD và điểm S không thuộc mp (ABCD). Có bao nhiêu mặt phẳng phân biệt xác định bởi 3 trong số các điểm A,B,C,D,S?
A. 5
B. 6
C. 7
D. 8
-
Câu 18:
Một hình không gian có hình chiếu đứng (nhìn từ trước vào (có thể nhìn từ sau) để từ hình 3D chuyển sang hình 2D) hình chiếu bằng (nhìn từ trên xuống) có thể nhìn từ dưới lên)), hình chiếu cạnh (từ trái sang (có thể nhìn từ phải sang)) lần lượt được thể hiện như sau:
Hãy vẽ hình biểu diễn của hình đó?
A.
B.
C.
D.
-
Câu 19:
Hình nào sau đây vẽ đúng quy tắc?
A.
B.
C.
D.
-
Câu 20:
Trong các mệnh đề sau mệnh đề nào sai?
A. Dùng nét đứt biểu diễn cho đường bị che khuất
B. Hình biểu diễn của đường thẳng là đường thẳng
C. Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng
D. Hình biểu diễn của hai đường cắt nhau có thể là hai đường song song
-
Câu 21:
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt..
B. Một điểm và một đường thẳng..
C. Hai đường thẳng cắt nhau..
D. Bốn điểm phân biệt.
-
Câu 22:
Cho 2 đường thẳng a,b cắt nhau và không đi qua điểm A . Xác định được nhiều nhất bao nhiêu mặt phẳng bởi a,b và A?
A. 1
B. 2
C. 3
D. 4
-
Câu 23:
Cho tứ diện SABC . Trên SA SB , và SC lấy các điểm D E , và F sao cho DE cắt AB tại I , EF cắt BC tại J , FD cắt CA tại K .Khẳng định nào sau đây đúng?
A. Ba điểm B,J, K thẳng hàng
B. Ba điểm I, J, K thẳng hàng
C. Ba điểm I, J, K không thẳng hàng
D. Ba điểm I, J,C thẳng hàng
-
Câu 24:
Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm AB và CD . Mặt phẳng (α) qua MN cắt AD và BC lần lượt tại P , Q . Biết MP cắt NQ tại I . Ba điểm nào sau đây thẳng hàng?
A. I , A , C .
B. I , B , D
C. I , A , B
D. I , C , D .
-
Câu 25:
Cho hình chóp S ABCD . có đáy ABCD là hình bình hành. Gọi I , J lần lượt là trung điểm SA và SB . Khẳng định nào sau đây là sai?
A. IJCD là hình thang.
B. (SAB)∩(IBC)=IB
C. (SBD)∩(JCD)=JD
D. (IAC)∩(JBD)=AO, O là tâm hình bình hành ABCD .
-
Câu 26:
Cho hình chóp S ABCD . có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm AD và BC . Giao tuyến của hai mặt phẳng (SMN) và (SAC) là:
A. SD .
B. SO , O là tâm hình bình hành ABCD .
C. SG , G là trung điểm AB .
D. SF , F là trung điểm CD .
-
Câu 27:
Cho hình chóp S.ABCD . Gọi I là trung điểm của SD , J là điểm trên SC và không trùng trung điểm SC . Giao tuyến của hai mặt phẳng (ABCD) và (AIJ) là:
A. AK , K là giao điểm IJ và BC .
B. AH , H là giao điểm IJ và AB .
C. AG , G là giao điểm IJ và AD .
D. AF , F là giao điểm IJ và CD .
-
Câu 28:
Cho tứ diện ABCD . Gọi O là một điểm bên trong tam giác BCD và M là một điểm trên đoạn AO . Gọi I, J là hai điểm trên cạnh BC , BD . Giả sử IJ cắt CD tại K , BO cắt IJ tại E và cắt CD tại H , ME cắt AH tại F . Giao tuyến của hai mặt phẳng (MIJ) và (ACD) là đường thẳng
A. KM
B. AK
C. MF
D. KF
-
Câu 29:
Cho hình chóp S.ABCD có đáy là hình thang ABCD (AB//CD) . Khẳng định nào sau đây sai?
A. Hình chóp S.ABCD có 4 mặt bên.
B. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là SO ( O là giao điểm của AC và BD ).
C. Giao tuyến của hai mặt phẳng (SAD) và (SBC) là SI ( I là giao điểm của AD và BC ).
D. Giao tuyến của hai mặt phẳng (SAB) và (SAD) là đường trung bình của ABCD .
-
Câu 30:
Cho tứ diện S. ABC Gọi M, N lần lượt là hai điểm trên cạnh AB và BC sao cho MN không song song với AC. Tìm giao tuyến của các cặp mặt phẳng sau (SMN) và (SAC)
A. SK với K là giao điểm AC và MN
B. SK với K là giao điểm AN và CM
C. SA
D. SB
-
Câu 31:
Cho hình chóp S.ABCD có AC∩BD=M và AB∩CD=N . Giao tuyến của mặt phẳng (SAC) và mặt phẳng ( SBD) là đường thẳng
A. SN.
B. SC
C. SB
D. SM
-
Câu 32:
Thiết diện của mặt phẳng với tứ diện
A. Tam giác hoặc tứ giác
B. Luôn là một tứ giác
C. Luôn là một tam giác
D. Tam giác hoặc tứ giác hoặc ngũ giác
-
Câu 33:
Cho ba đường thẳng a, b, c đôi một cắt nhau và không đồng phẳng. Số giao điểm của ba đường thẳng là:
A. 3
B. 6
C. 1
D. Kết quả khác
-
Câu 34:
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
A. Ba đường thẳng A’B’, AB, CD đồng quy
B. Ba đường thẳng A’B’, AB, CD đồng quy hoặc đôi một song song
C. Trong ba đường thẳng A’B’, AB, CD có hai đường thẳng không thể cùng thuộc một mặt phẳng.
D. Ba đường thẳng A’B’, AB, CD đồng quy tại điểm thuộc mặt phẳng (SBC).
-
Câu 35:
Cho hình chóp S.ABCD, đáy là hình thang ABCD, AD // BC và AD > BC, A’ là trung điểm của SA, B’ thuộc cạnh SB và không phải là trung điểm của SB. Phát biểu nào sau đây là đúng?
A. Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tam giác A’B’C.
B. Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tứ giác A’BCD
C. Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tứ giác A’B’CA
D. Thiết diện của mặt phẳng (A’B’C) với hình chóp S.ABCD là tứ giác A’B’CD
-
Câu 36:
Cho hình chóp S. ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biều nào sau đây là đúng?
A. Thiết diện của (MND) với hình chóp là tam giác MND
B. Thiết diện của (MND) với hình chóp là tứ giác NDMK, với K là giao điểm của SB với NI, I là giao điểm của MD với BC
C. Thiết diện của (MND) với hình chóp là tứ giác NDMB
D. Thiết diện của (MND) với hình chóp là tam giác NDB.
-
Câu 37:
Cho hình chóp S.ABCD, đáy là hình bình hành ABCD, các điểm M, N lần lượt thuộc các cạnh AB, SC. Phát biểu nào sau đây là đúng?
A. Giao điểm của MN với (SBD) là giao điểm của MN với BD.
B. Đường thẳng MN không cắt mặt phẳng (SBD)
C. Giao điểm của MN với (SBD) là giao điểm của MN với SI, trong đó I là giao điểm của CM với BD
D. Giao điểm của MN với (SBD) là M.
-
Câu 38:
Cho hình chóp S.ABCD, các điểm A’, B’, C’ lần lượt thuộc các cạnh SA, SB, SC. Phát biểu nào sau đây là đúng?
A. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tam giác A’B’C’
B. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác A’B’C’D’ với D’ là giao điểm của B’I với SD, trong đó I là giao điểm của A’C’ với SO, O là giao điểm của AC và BD
C. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác SA’B’C’
D. Thiết diện của (A’B’C’) với hình chóp S.ABCD là tứ giác A’B’C’D
-
Câu 39:
Cho hình chóp S.ABCD, M là điểm nằm trong tam giác SAD. Phát biểu nào sau đây là đúng?
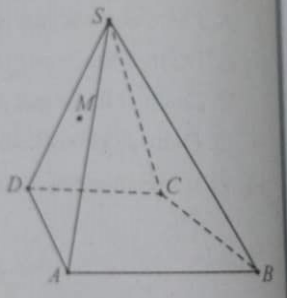
A. Giao điểm của (SMC) với BD là giao điểm của CN với BD, trong đó N là giao điểm của SM và AD.
B. Giao điểm của (SAC) với BD là giao điểm của SA và BD
C. Giao điểm của (SAB) với CM là giao điểm của SA và CM
D. Đường thẳng DM không cắt mặt phẳng (SBC)
-
Câu 40:
Cho hình chóp O.ABC, A’ là trung điểm của OA, B’, C’ tương ứng thuộc các cạnh OB, OC và không phải là trung điểm của các cạnh này. Phát biểu nào sau đây là đúng?
A. Đường thẳng AC và A’C’ cắt nhau.
B. Đường thẳng OA và C’B’ cắt nhau.
C. Hai đường thẳng AC và A’C’ cắt nhau tại một điểm thuộc (ABO)
D. Hai đường thẳng CB và C’B’ cắt nhau tại một điểm thuộc (OAB)
-
Câu 41:
Cho hình chóp S.ABCDE, phát biều nào sau đây là đúng?
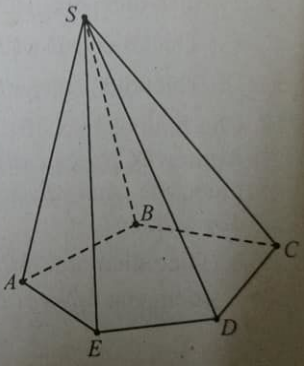
A. SE và AB cắt nhau
B. Đường thẳng SB nằm trong mặt phẳng SED
C. (SAE) và (SBC) có một điểm chung duy nhất
D. SD và BC chéo nhau.
-
Câu 42:
Phát biểu nào sau đây là đúng?
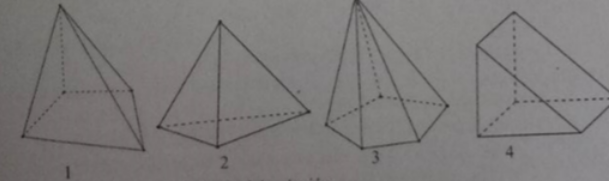
A. Hình 1 và hình 4 là các hình chóp tứ giác
B. Hình 2 và hình 4 là các hình chóp tam giác
C. Hình 1,2,3 là các hình chóp
D. Hình 3,4 không phải là hình chóp.
-
Câu 43:
Cho hình chóp S.ABCDE, phát biểu nào sau đây là đúng.
A. Điểm B thuộc mặt phẳng (SED)
B. Điểm E thuộc mặt phẳng (SAB)
C. Điểm D thuộc mặt phẳng (SBC)
D. Điểm B thuộc mặt phẳng (SAB)
-
Câu 44:
Trong các hình sau, hình nào là hình chóp.
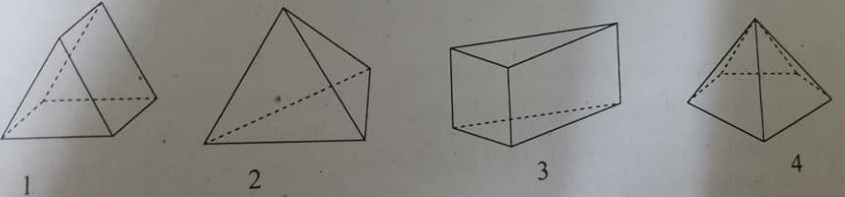
A. Hình 1,2 và 4
B. hình 2 và 4
C. hình 2 và 3
D. tất cả các hình trên.
-
Câu 45:
Có ít nhất bao nhiêu điểm không cùng thuộc một mặt phẳng?
A. 1
B. 2
C. 3
D. 4
-
Câu 46:
Cho 4 điểm không đồng phẳng. Số mặt phẳng phân biệt mà mỗi mặt phẳng đi qua ba trong bốn điểm đó là:
A. 1
B. 2
C. 3
D. 4
-
Câu 47:
Hai đường thẳng chéo nhau nếu.
A. Chúng không có điểm chung
B. Chúng không cắt nhau và không song song với nhau
C. Chúng không cùng nằm trong bất kì một mặt phẳng nào
D. Chúng không nằm trong bất cứ hai mặt phẳng nào cắt nhau.
-
Câu 48:
Có một và chỉ một mặt phẳng đi qua
A. Ba điểm
B. Một điểm và một đường thẳng không chứa điểm đó.
C. Hai điểm
D. Bốn điển
-
Câu 49:
Có duy nhất một mặt phẳng đi qua
A. Hai đường thẳng
B. Một điểm và một đường thẳng
C. Ba điểm
D. Hai đường thẳng cắt nhau
-
Câu 50:
Cho 4 điểm không cùng thuộc một mặt phẳng. Trong các phát biểu sau đây, phát biểu nào là sai?
A. Trong 4 điểm đã cho không có ba điểm nào thẳng hàng
B. Trong 4 điểm đã cho luôn luôn tồn tại 3 điểm thuộc cùng 1 mặt phẳng
C. Số mặt phẳng đi qua 3 trong 4 điểm đã cho là 4
D. Số đoạn thẳng nối hai điểm trong 4 điểm đã cho là 6.



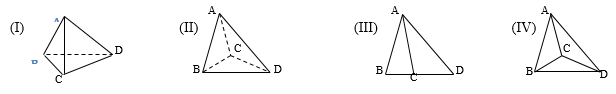
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)











