Câu hỏi:
Hình dưới là sơ đồ tạo ảnh của vật sáng AB qua thấu kính hội tụ. Cho biết vật AB có chiều cao cm; ảnh cao cm và khoảng cách OA = 15 cm.
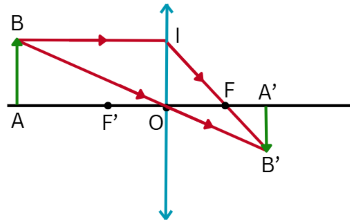
Tiêu cự của thấu kính là bao nhiêu cm? (làm tròn kết quả đến hàng phần mười)
Đáp án đúng: 6,7
Ta có
\({\rm{\Delta }}OB'F \sim {\rm{\Delta }}BB'I\)
Suy ra
\(\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}}\)
Mà
\(\frac{{BB'}}{{OB'}} = \frac{{OB + OB'}}{{OB'}} = \frac{{OB}}{{OB'}} + 1 = \frac{{AB}}{{A'B'}} + 1 = 2,25\)
Suy ra
\(\frac{{BI}}{{OF}} = 2,25 \to OF = \frac{{BI}}{{2,25}} = \frac{{15}}{{2,25}} = 6,7cm\)
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề Kiểm Tra Tham Khảo Học Kì 1 - Môn Khoa Học Tự Nhiên 9 - Cánh Diều giúp học sinh đánh giá khả năng tiếp thu và vận dụng kiến thức đã học trong học kỳ, qua các dạng bài tập từ cơ bản đến nâng cao. Đề thi này không chỉ kiểm tra kiến thức mà còn giúp rèn luyện khả năng giải quyết vấn đề nhanh chóng.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026
