Một đồng hồ có kim phút và kim giờ. Phát biểu nào sau đây là đúng:

Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 12 lần

Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 24 lần

Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 23 lần

Trong nột ngày đêm (24h), kim giờ và kim phút gặp (trùng) nhau 22 lần

Trả lời:

Đáp án đúng: D

Trong 12 giờ, kim phút vượt kim giờ 11 lần. Vì vậy, trong 24 giờ (một ngày đêm), kim phút vượt kim giờ 22 lần, tức là chúng gặp nhau 22 lần.

520+ câu hỏi trắc nghiệm Vật lí đại cương kèm đáp án và lời giải minh họa - Phần 4

500+ câu hỏi ôn tập trắc nghiệm môn Vật lý đại cương sẽ là đề cương ôn thi hữu ích dành cho các bạn sinh viên Đại học - Cao đẳng ôn thi môn đại cương dễ dàng hơn. Mời các bạn cùng tham khảo!

50 câu hỏi 60 phút

Bắt đầu thi

Câu hỏi liên quan

Câu 32:

Một dây cuaroa truyền động, vòng qua vô lăng I và bánh xe II (hình 3.9). Bán kính của vô lăng và bánh xe là R₁ = 10cm và R₂ = 50cm. Vô lăng đang quay với vận tốc 720 vòng/phút thì bị ngắt điện, nó quay chậm dần đều, sau đó 30 giây vận tốc chỉ còn 180 vòng/phút. Vận tốc quay của bánh xe ngay trước khi ngắt điện là:

Lời giải:

Đáp án đúng: B

Vì dây cuaroa truyền động nên vận tốc dài của hai điểm trên vành của vô lăng và bánh xe là bằng nhau. Ta có: v1 = v2 => R1*ω1 = R2*ω2. Với ω1 = 720 vòng/phút = 720/60 vòng/giây = 12 vòng/giây. Suy ra ω2 = (R1/R2)*ω1 = (10/50)*12 = 2.4 vòng/giây = 2.4 * 60 vòng/phút = 144 vòng/phút.

Câu 33:

Cho tam giác đều ABC, cạnh a. Đặt tại các đỉnh A, B, C các chất điểm có khối lượng bằng nhau và bằng m. Đặt thêm một chất điểm có khối lượng 3m tại A. Mômen quán tính đối với trục quay đi qua khối tâm của hệ và vuông góc với mặt phẳng (ABC) là:

Lời giải:

Đáp án đúng: C

Gọi G là trọng tâm tam giác ABC, đồng thời cũng là khối tâm của hệ (do khối lượng các chất điểm tại B và C bằng nhau và bằng m, khối lượng tại A là m + 3m = 4m).

Khoảng cách từ G đến mỗi đỉnh A, B, C là: r = a\/\/\/3.

Mômen quán tính của hệ đối với trục quay đi qua G và vuông góc với mặt phẳng (ABC) là:

I = m_Ar² + m_Br² + m_Cr² + 3m_Ar²

I = 4m(a\/\/\/3)² + m(a\/\/\/3)² + m(a\/\/\/3)²

I = 4ma²\/3 + ma²\/3 + ma²\/3 = 2ma².

Câu 34:

Một quả cầu đặc đồng chất, tâm O, bán kính R, khối lượng m phân bố đều, được gắn chặt tiếp xúc ngòai với một quả cầu đặc khác, tâm O’, đồng chất với nó nhưng có bán kính gấp đôi. Mômen quán tính của hệ hai quả cầu này đối với trục quay chứa O và O’ là:

Lời giải:

Đáp án đúng: A

Gọi I1 là moment quán tính của quả cầu nhỏ (bán kính R, khối lượng m) đối với trục quay đi qua O và O'. Theo định lý Steiner, ta có: I1 = (2/5)mR^2 + mR^2 = (7/5)mR^2.

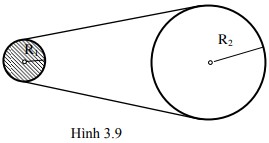
Gọi I2 là moment quán tính của quả cầu lớn (bán kính 2R, khối lượng 8m) đối với trục quay đi qua O và O'. Theo định lý Steiner, ta có: I2 = (2/5)(8m)(2R)^2 + 8m(3R)^2 = (64/5)mR^2 + 72mR^2 = (424/5)mR^2.

Moment quán tính của hệ hai quả cầu là I = I1 + I2 = (7/5)mR^2 + (424/5)mR^2 = (431/5)mR^2. Kiểm tra lại bài toán, xem xét quả cầu lớn có bán kính 2R và khối lượng 8m (do tỉ lệ với thể tích). Khoảng cách từ tâm O' đến trục quay là 3R. Khi đó:
I2 = (2/5)*(8m)*(2R)^2 + 8m*(3R)^2 = (64/5)mR^2 + 72mR^2 = (64/5 + 360/5)mR^2 = (424/5)mR^2.
Tổng moment quán tính: I = I1 + I2 = (7/5)mR^2 + (424/5)mR^2 = (431/5)mR^2.

Tuy nhiên, không có đáp án nào trùng với kết quả này. Có thể có lỗi trong đề bài hoặc trong các phương án trả lời. Đề bài yêu cầu trục quay chứa O và O'. Nếu hiểu là trục quay đi qua tâm của cả hai quả cầu, thì công thức tính sẽ khác. Trong trường hợp đó, moment quán tính của quả cầu nhỏ là (2/5)mR^2, moment quán tính của quả cầu lớn là (2/5)(8m)(2R)^2 = (64/5)mR^2. Tổng moment quán tính là (2/5)mR^2 + (64/5)mR^2 = (66/5)mR^2.

Với cách hiểu này, đáp án đúng là (66/5)mR^2.

Câu 35:

Một đĩa tròn mỏng đồng chất, khối lượng phân bố đều, bán kính R, bị khoét một lỗ hình tròn, bán kính r = R/2. Tâm O’ của lỗ thủng cách tâm O của đĩa một khoảng R/2. Khối lượng của phần còn lại là m. Mômen quán tính của phần còn lại đối với trục quay đi qua tâm O và vuông góc với mặt phẳng đĩa là:

Lời giải:

Đáp án đúng: C

Gọi \(M\) là khối lượng của đĩa tròn lớn (chưa khoét lỗ). Diện tích của đĩa lớn là \(\pi R^2\), diện tích của lỗ tròn là \(\pi (R/2)^2 = \frac{1}{4}\pi R^2\). Do đó, diện tích phần còn lại là \(\frac{3}{4}\pi R^2\). Vì đĩa đồng chất nên khối lượng tỉ lệ với diện tích. Ta có: \(m = \frac{3}{4}M\), suy ra \(M = \frac{4}{3}m\).\nMômen quán tính của đĩa lớn đối với trục quay đi qua tâm O và vuông góc với mặt phẳng đĩa là \(I_1 = \frac{1}{2}MR^2 = \frac{1}{2}(\frac{4}{3}m)R^2 = \frac{2}{3}mR^2\).\nMômen quán tính của phần bị khoét (lỗ tròn) đối với trục quay đi qua tâm O' và vuông góc với mặt phẳng đĩa là \(I_{2O'} = \frac{1}{2}m'(R/2)^2\), trong đó \(m'\) là khối lượng của phần bị khoét. Ta có \(m' = \frac{1}{4}M = \frac{1}{4}(\frac{4}{3}m) = \frac{1}{3}m\). Suy ra \(I_{2O'} = \frac{1}{2}(\frac{1}{3}m)(\frac{R}{2})^2 = \frac{1}{24}mR^2\).\nÁp dụng định lý Steiner, mômen quán tính của phần bị khoét đối với trục quay đi qua tâm O và vuông góc với mặt phẳng đĩa là \(I_2 = I_{2O'} + m'(R/2)^2 = \frac{1}{24}mR^2 + \frac{1}{3}m(\frac{R}{2})^2 = \frac{1}{24}mR^2 + \frac{1}{12}mR^2 = \frac{1}{8}mR^2\).\nMômen quán tính của phần còn lại là \(I = I_1 - I_2 = \frac{2}{3}mR^2 - \frac{1}{8}mR^2 = (\frac{2}{3} - \frac{1}{8})mR^2 = (\frac{16}{24} - \frac{3}{24})mR^2 = \frac{13}{24}mR^2\).

Câu 37:

Bốn quả cầu nhỏ giống nhau, mỗi quả cầu (coi như chất điểm) có khối lượng 0,5kg đặt ở các đỉnh một hình vuông cạnh 2m và được giữ cố định ở đó bằng bốn thanh không khối lượng, các thanh này chính là cạnh hình vuông. Mômen quán tính của hệ này đối với trục quay ∆ đi qua trung điểm của hai cạnh đối diện là:

Lời giải:

Đáp án đúng: B

Mômen quán tính của một chất điểm đối với một trục quay được tính bằng công thức I = mr², trong đó m là khối lượng của chất điểm và r là khoảng cách từ chất điểm đến trục quay.

Trong trường hợp này, ta có bốn quả cầu nhỏ đặt ở các đỉnh của một hình vuông cạnh 2m. Trục quay đi qua trung điểm của hai cạnh đối diện của hình vuông. Khoảng cách từ mỗi quả cầu đến trục quay là một nửa độ dài cạnh của hình vuông, tức là 1m.

Do đó, mômen quán tính của mỗi quả cầu đối với trục quay là I = mr² = 0,5kg * (1m)² = 0,5 kgm².

Vì có bốn quả cầu, mômen quán tính của cả hệ là tổng mômen quán tính của từng quả cầu:

I_hệ = 4 * 0,5 kgm² = 2 kgm².

Vậy đáp án đúng là 2 kgm².

Câu 38:

Khối hình hộp chữ nhật, mỏng, khối lượng m phân bố đều, chiều rộng là a, chiều dài b. Mômen quán tính đối với trục quay qua tâm và vuông góc mặt phẳng hình chữ nhật là:

Lời giải: