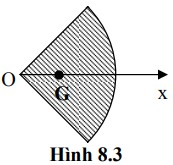
Một cái đĩa đồng chất, dao động trong mặt phẳng thẳng đứng, quanh một trục nằm ngang đi qua một điểm trên mép đĩa. Tính chu kì dao động nhỏ của thước theo bán kính R của đĩa (lấy g = 9,8 m/s2, π2 = 9,8).
Đáp án đúng: A
Chu kì dao động của con lắc vật lý được tính theo công thức: \(T = 2\pi \sqrt{\frac{I}{mgd}}\), trong đó I là moment quán tính của vật đối với trục quay, m là khối lượng của vật, g là gia tốc trọng trường, và d là khoảng cách từ trục quay đến trọng tâm của vật.
Trong trường hợp này, vật là một đĩa đồng chất, trục quay nằm trên mép đĩa, và trọng tâm của đĩa nằm ở tâm của nó. Moment quán tính của đĩa đối với trục quay đi qua tâm là \(I_c = \frac{1}{2}mR^2\). Theo định lý Steiner (hay còn gọi là định lý Huygens-Steiner), moment quán tính đối với trục quay ở mép đĩa là \(I = I_c + md^2 = \frac{1}{2}mR^2 + mR^2 = \frac{3}{2}mR^2\). Khoảng cách d từ trục quay đến trọng tâm là R.
Thay các giá trị vào công thức chu kì, ta có: \(T = 2\pi \sqrt{\frac{\frac{3}{2}mR^2}{mgR}} = 2\pi \sqrt{\frac{3R}{2g}}\).
Vì \(\pi^2 = g = 9.8\), ta có: \(T = 2\pi \sqrt{\frac{3R}{2\pi^2}} = 2\sqrt{\frac{3R}{2}} = \sqrt{6R}\)
Vậy đáp án đúng là \(T = \sqrt{6R}\).
500+ câu hỏi ôn tập trắc nghiệm môn Vật lý đại cương sẽ là đề cương ôn thi hữu ích dành cho các bạn sinh viên Đại học - Cao đẳng ôn thi môn đại cương dễ dàng hơn. Mời các bạn cùng tham khảo!
Câu hỏi liên quan
- Ô tô đi vào garage: Kích thước ô tô quan trọng so với kích thước garage.
- Xe lửa từ Sài Gòn đến Nha Trang: Kích thước xe lửa nhỏ bé so với quãng đường dài từ Sài Gòn đến Nha Trang. Do đó, có thể xem xe lửa là chất điểm.
- Con sâu rọm bò trên lá khoai lang: Kích thước sâu rọm đáng kể so với lá khoai lang.
- Cái võng đu đưa: Kích thước võng quan trọng để mô tả chuyển động.
Vậy, đáp án đúng là xe lửa từ Sài Gòn đến Nha Trang.
.jpg)
