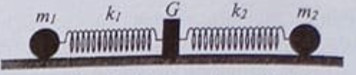
Hình bên mô tả một hệ gồm hai con lắc lò xo nằm ngang, đồng trục cùng được gắn vào giá G. Các lò xo nhẹ k1 và k2 có độ cứng lần lượt là 32 N/m và 12 N/m. Các vật nhỏ m1 và m2 có khối lượng lần lượt là 512 g và 192 g. Đưa hai vật đến các vị trí sao cho cả hai lò xo cùng dãn 15 cm rồi thả nhẹ m1 để m1 dao động điều hòa. Sau khi thả m1 một khoảng thời gian \(\Delta t\) thì thả nhẹ m2 để m2 dao động điều hòa. Biết rằng G được gắn với sàn, G không bị trượt trên sàn khi hợp lực của các lực đàn hồi của hai lò xo tác dụng vào G có độ lớn không vượt quá 4,2 N. Lấy \({\pi ^2} = 10\). Giá trị lớn nhất của \(\Delta t\) để G không bao giờ bị trượt trên sàn là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai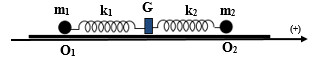
Chọn trục Ox có chiều dương như hình vẽ:
Chọn gốc thời gian là lúc m1 bắt đầu dao động
Vật m1 dao động quanh vị trí cân bằng O1, m2 dao động quanh vị trí cân bằng O2 với :
- tần số góc: \(\omega = \sqrt {\frac{{{k_1}}}{{{m_1}}}} = \,\sqrt {\frac{{{k_1}}}{{{m_1}}}} \,\, = 2,5\pi \,\,rad/s\)
- Biên độ : A = 15 cm
Phương trình dao động của m1 và m2 : \(\left\{ \begin{array}{l}
{x_1} = A\cos \left( {\omega t + \pi } \right)\\
{x_2} = A\cos \left( {\omega \left( {t - \Delta t} \right)} \right)
\end{array} \right.\)
( m1 bắt từ từ biên âm, m2 bắt đầu từ biên dương)
Lực đàn hồi của mỗi lò xo:
+ \({F_1} = - {k_1}.{x_1} = - 4,8\cos \left( {\omega t + \pi } \right) = 4,8\cos (\omega t)\)
+ \({F_2} = - {k_2}.{x_2} = - 1,8\cos \left( {\omega t - \omega .\Delta t} \right) = 1,8\cos \left( {\omega t - \varphi } \right)\), với \(\varphi = \omega .\Delta t + \pi \)
Lực đàn hồi tác dụng vào giá G:
F = F1 + F2 = \(4,8\cos \left( {\omega t} \right) + 1,8\cos \left( {\omega t - \varphi } \right)\)
Để giá G không trượt thì biên độ Fo thỏa mãn:
\({F_o}^2 = 4,{8^2} + 1,{8^2} + 2.4,8.1,8.\cos \varphi \le 4,{2^2}\) \(\Leftrightarrow \cos \varphi \le \,\, - \,0,5\)
Vì Δt có giá trị lớn nhất, nên ta chọn φmax = ω.Δtmax + π = \(\frac{{4\pi }}{3}\)
\(\Rightarrow \,\,\Delta {t_{\max }} = \frac{\pi }{{3.\omega }} = \frac{2}{{15}}\,\,s\).
Đáp án A














