Cho hình lăng trụ \(ABC.A'B'C'\) có \(AA'=\frac{a\sqrt{10}}{4},\,AC=a\sqrt{2},\,BC=a,\,\,\widehat{ACB}={{135}^{0}}\). Hình chiếu vuông góc của C’ lên mặt phẳng (ABC) trùng với trung điểm M của AB. Góc tạo thành bởi đường thẳng C’M với mặt phẳng (ACC’A’) bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai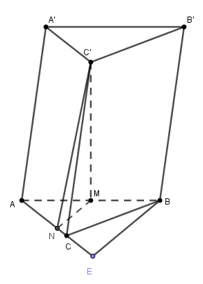
Kẻ \(BE,\,\,MN\) vuông góc với AC.
\(\Delta BEC\) vuông tại E \(\Rightarrow BE=BC.\sin \widehat{BCE}=a.\sin {{45}^{0}}=\frac{a\sqrt{2}}{2}\)
\(MN\bot AC,\,\,BE\bot AC\Rightarrow MN//BE\), mà M là trung điểm của AB
\(\Rightarrow \)MN là đường trung bình của tam giác ABE \(\Rightarrow MN=\frac{BE}{2}=\frac{a\sqrt{2}}{4}\)
Ta có: \(\left\{ \begin{align} & AC\bot MN \\ & AC\bot C'M \\\end{align} \right.\Rightarrow AC\bot (C'MN)\Rightarrow (ACC'A')\bot (C'MN)\)
Mà \((ACC'A')\cap (C'MN)=C'N\Rightarrow \left( \widehat{C'M;(ACC'A')} \right)=\left( \widehat{C'M;C'N} \right)\)
Xét \(\Delta ABC\):\(A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}}-2.AB.BC.\cos C=2{{a}^{2}}+{{a}^{2}}-2.\sqrt{2}a.a.\cos {{135}^{0}}=5{{a}^{2}}\)
ME là trung tuyến của tam giác ABE \(\Rightarrow M{{C}^{2}}=\frac{2(A{{C}^{2}}+B{{C}^{2}})-A{{B}^{2}}}{4}=\frac{2(2{{a}^{2}}+{{a}^{2}})-5{{a}^{2}}}{4}=\frac{{{a}^{2}}}{4}\Rightarrow CM=\frac{a}{2}\)
\(\Delta CMC'\) vuông tại M \(\Rightarrow C'M=\sqrt{CC{{'}^{2}}-C{{M}^{2}}}=\sqrt{{{\left( \frac{a\sqrt{10}}{4} \right)}^{2}}-{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{6}}{4}\)
\(\Delta C'MN\) vuông tại M \(\Rightarrow \tan \widehat{NC'M}=\frac{MN}{C'M}=\frac{\frac{a\sqrt{2}}{4}}{\frac{a\sqrt{6}}{4}}=\frac{1}{\sqrt{3}}\Rightarrow \widehat{NC'M}={{30}^{0}}\Rightarrow \) \(\left( \widehat{C'M;(ACC'A')} \right)={{30}^{0}}\)
Chọn: C
Đề thi thử THPT QG năm 2023 môn Toán
Trường THPT Nguyễn Hữu Thọ
Câu hỏi liên quan
-
Cho hàm số \(y=f(x)\) liên tục trên R và có bảng biến thiên dưới đây
.png)
Hàm số có giá trị cực tiểu là:
-
Cho hình chóp S.ABCD, có đáy là hình chữ nhật, \(AB=a,\,\,AD=2a\), cạnh bên \(SA=a\) và \(SA\) vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBD) bằng
-
Biết \(\int\limits_{1}^{2}{\dfrac{3{{x}^{2}}+5x+4}{{{x}^{2}}+x+1}dx=a+b\ln 7+c\ln 3}\) (a,b,c là các số nguyên) khi đó \(a+b+c\) bằng
-
Cho hình chóp \(S.ABCD\), tứ giác \(ABCD\) đáy là hình thang vuông tại \(A\) và \(B\), \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Biết \(AB = 2CD = 2AD\). Mệnh đề nào sau đây sai?
-
Tập hợp giá trị m để hàm số \(y=\frac{1}{3}({{m}^{2}}-1){{x}^{3}}+(m+1){{x}^{2}}+3x-1\) đồng biến trên \(\mathbb{R}\) là:
-
Cho hàm số \(y=f(x)\). Hàm số \(y=f'(x)\) là hàm số bậc ba có đồ thị như hình vẽ. Hàm số \(g(x)=f\left( -{{x}^{2}}+3 \right)\). Mệnh đề nào dưới đây đúng?
.png)
-
Cho hàm số \(y=f(x)={{x}^{3}}-3{{x}^{2}}-4x\,\,(C)\). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số (C) và trục hoành. Phát biểu nào sau đây đúng?
-
Với m là tham số thực dương khác 1, tập nghiệm của bất phương trình \({{\log }_{m}}\left( 2{{x}^{2}}+x+3 \right)\le {{\log }_{m}}\left( 3{{x}^{2}}-x \right)\)là tập \(S=\left[ a;b \right)\cup \left( c;d \right]\). Biết \(x=1\) là một nghiệm của bất phương trình, khi đó \(a+b+c+d\) bằng
-
Cho hình phẳng D giới hạn bởi đường cong \(y=2x-{{x}^{2}}\), trục hoành và các đường thẳng \(x=0,\,\,x=2\). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích:
-
Cho hình nón có bán kính đáy \(r=a\), chiều cao là \(h=3a\), thể tích của khối nón bằng
-
Trong không gian \(Oxyz\,\)cho đường thẳng \(d:\left\{ \begin{align} & x=1+2t \\ & y=-1+3t \\ & z=-t \\\end{align} \right.\). Trong các điểm sau điểm nào không thuộc d ?
-
Trong mặt phẳng với hệ trục tọa độ \(Oxy\). Cho đường tròn \(\left( C \right)\) có phương trình: \({\left( {x - 1} \right)^2} + {\left( {y - 5} \right)^2} = 4\) và điểm \(I\left( {2; - 3} \right).\) Gọi \(\left( {C'} \right)\) là ảnh của \(\left( C \right)\) qua phép vị tự \(V\) tâm \(I\) tỉ số \(k = - 2.\) Tìm phương trình của \(\left( {C'} \right).\)
-
Một người gửi 50 triệu đồng vào ngân hàng với lãi suất \(6%/\)năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau 3 năm người đó nhận được bao nhiêu tiên? Biết trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra.
-
Hàm số \(y=\frac{x+3}{x-2}\) nghịch biến trên các khoảng:
-
Một hộp chứa 3 viên bi xanh, 2 viên bi vàng, 1 viên bi trắng. Lấy ngẫu nhiên 3 viên bi. Xác suất để lấy ra 3 viên bi có đủ 3 màu là:
-
Cho hàm số \(y=\frac{2x+2}{x-1}\) có đồ thị (C). Đường thẳng (d): \(y=x+1\) cắt đồ thị (C) tại 2 điểm phân biệt M và N thì tung độ trung điểm I của đoạn thẳng MN bằng
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh SA vuông góc với mặt đáy (ABC) và \(SA=\sqrt{3}a\). Thể tích khối chóp S.ABC bằng:
-
Cho \(0\le x;\,y\le 1\) thỏa mãn \(\frac{{{2018}^{1-x}}}{{{2018}^{y}}}=\frac{{{x}^{2}}+2019}{{{y}^{2}}-2y+2020}\). Gọi M, m lần lượt là GTLN, GTNN của biểu thức \(P=\left( 4{{x}^{2}}+3y \right)\left( 4{{y}^{2}}+3x \right)+25xy\), khi đó \(M+m\) bằng bao nhiêu?
-
Cho hàm số \(f(x)\) có \(f'(x)=\left\{ \begin{align} & \frac{-x}{\sqrt{4-{{x}^{2}}}},\,\,0\le x\le 1 \\ & \frac{-\sqrt{3}}{3}x\,\,\,\,,x>1 \\\end{align} \right.\) và \(f(1)=\sqrt{3}\). Khi đó, kết quả \(\int\limits_{0}^{2}{f(x)dx}\) là:
-
Cho hình trụ (T) có \(\left( C \right),\,\,\left( C' \right)\) là hai đường tròn đáy nội tiếp hai mặt đối diện của một hình lập phương. Biết rằng, trong tam giác cong tạo bởi đường tròn (C) và hình vuông ngoại tiếp của (C) có một hình chữ nhật kích thước \(1\times 2\) (như hình vẽ dưới đây). Thể tích của khối trụ (T) là:
.png)
