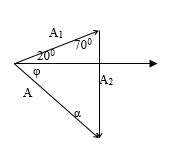
Cho hai dao động điều hòa cùng phương với các phương trình lần lượt là   ${x_1} = {A_1}\cos \left( {\omega t + 0,35} \right)cm;{x_2} = {A_2}\cos \left( {\omega t - 1,57} \right)cm$. Dao động tổng hợp của hai dao động này có phương trình là  $x = 20\cos \left( {\omega t + \varphi } \right)cm$. Giá trị cực đại của (A₁ + A₂) gần giá trị nào nhất sau đây? 

Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch AB mắc nối tiếp (hình vẽ). Biết tụ điện có dung kháng Z_C, cuộn cảm thuần có cảm kháng Z_L và 3Z_L = 2Z_C. Đồ thị biểu diễn sự phụ thuộc vào thời gian của điện áp giữa hai đầu đoạn mạch AN và điện áp giữa hai đầu đoạn mạch MB như hình vẽ. Điệp áp hiệu dụng giữa hai điểm M và N là 

Chùm ánh sáng laze không được ứng dụng 

Trong phản ứng hạt nhân không có sự bảo toàn 

Một học sinh làm thực hành xác định số vòng dây của hai máy biến áp lí tưởng A và B có các duộn dây với số vòng dây (là số nguyên) lần lượt là N_1A, N_2A, N_1B, N_2B. Biết N_2A = kN_1A; N_2B = 2kN_1B; k > 1; N_1A + N_2A + N_1B + N_­2B = 3100 vòng và trong bốn cuộn dây có hai cuộn có số vòng dây đều bằng N. Dùng kết hợp hai máy biến áp này thì có thể tăng điện áp hiệu dụng U thành 18U hoặc 2U. Số vòng dây N là 

Một tụ điện có điện dung C tích điện Q₀. Nếu nối tụ điện với cuộn cảm thuần có độ tự cảm L₁ hoặc với cuộn cảm thuần có độ tự cảm L₂ thì trong mạch có dao động điện từ tự do với cường độ dòng điện cực đại là 20mA hoặc 10mA. Nếu nối tụ điện với cuộn cảm thuần có độ tự cảm ${L_3} = 9{L_1} + 4{L_2}$ thì trong mạch có dao động điện từ tự do với cường độ dòng điện cực đại là 

Một đoạn mạch điện xoay chiều gồm điện trở thuần R mắc nối tiếp với một cuộn cảm thuần có cảm kháng với giá trị bằng R. Độ lệch pha của điện áp giữa hai đầu đoạn mạch với cường độ dòng điện trong mạch bằng 

Đồng vị là những nguyên tử mà hạt nhân có cùng số 

Đặt điện áp xoay chiều có giá trị hiệu dụng 200V và tần số không thay đổi vào hai đầu đoạn mạch AB (hình vẽ). Cuộn cảm thuần có độ tự cảm L xác định; R = 200Ω; tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung C để điện áp hiệu dụng giữa hai đầu đoạn mạch MB đạt giá trị cực tiểu là U₁ và giá trị cực đại là U₂ = 400V. Giá trị của U₁ là 

Đặt điện áp $u = {U_0}\cos \left( {100\pi t + \frac{\pi }{4}} \right)V$ vào hai đầu đoạn mạch chỉ có tụ điện thì cường độ dòng điện trong mạch là $i = {I_0}\cos \left( {100\pi t + \varphi } \right)A$. Giá trị của  φ  bằng 

Tia α 

Một mạch dao động LC lí tưởng đang có dao động điện từ tự do với điện tích cực đại của tụ điện là Q₀ và cường độ dòng điện cực đại trong mạch là I₀. Dao động điện từ tự do trong mạch có chu kì là 

Gọi n_đ, n_t và n_v lần lượt là chiết suất của một môi trường trong suốt đối với các ánh sáng đơn sắc đỏ, tím và vàng. Sắp xếp nào sau đây là đúng? 

Một con lắc lò xo treo vào một điểm cố định, dao động điều hòa theo phương thẳng đứng với chu kì 1,2s. Trong một chu kì, nếu tỉ số của thời gian lò xo giãn với thời gian lò xo nén bằng 2 thì thời gian mà lực đàn hồi ngược chiều lực kéo về là 

Một vật có khối lượng 50g, dao động điều hòa với biên độ 4 cm và tần số góc 3rad/s. Động năng cực đại của vật là 

Trong chân không, một ánh sáng có bước sóng là 0,60mm. Năng lượng của phôtôn ánh sáng này bằng 

Đặt điện áp $u = 180\sqrt 2 \cos \left( {\omega t} \right)V$ (với $\omega$ không đổi) vào hai đầu đoạn mạch AB (hình vẽ). R là điện trở thuần, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L thay đổi được. Điện áp hiệu dụng ở hai đầu đoạn mạch MB và độ lớn góc lệch pha của cường độ dòng điện so với điện áp u khi L= L₁ là U và j₁, còn khi L = L₂ thì tương ứng là $\sqrt 8 U$ và j₂. Biết ${\varphi _1} + {\varphi _2} = {90^0}$. Giá trị U bằng 

Một sóng cơ truyền dọc theo một sợi dây đàn hồi rất dài với biên độ 6mm. Tại một thời điểm, hai phần tử trên dây cùng lệch khỏi vị trí cân bằng 3mm, chuyển động ngược chiều và cách nhau một khoảng ngắn nhất là 8cm (tính theo phương truyền sóng). Gọi d là tỉ số của tốc độ dao động cực đại của một phần tử trên dây với tốc độ truyền sóng. d gần giá trị nào nhất sau đây? 

Hai mạch dao động điện từ LC lí tưởng đang có dao động điện từ tự do với các cường độ dòng điện tức thời trong hai mạch là i1 và i2 được biểu diễn như hình vẽ. Tổng điện tích của hai tụ điện trong hai mạch ở cùng một thời điểm có giá trị lớn nhất bằng 

Một con lắc đơn dao động điều hòa với biên độ góc 0,1rad; tần số góc 10rad/s và pha ban đầu 0,79rad. Phương trình dao động của con lắc là

Trong các hạt nhân nguyên tử:  ${}_2^4He;{}_{26}^{56}Fe;{}_{92}^{238}U;{}_{90}^{230}Th$, hạt nhân bền vững nhất là