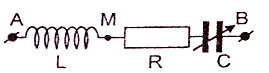
Đặt điện áp xoay chiều có giá trị hiệu dụng 200V và tần số không thay đổi vào hai đầu đoạn mạch AB (hình vẽ). Cuộn cảm thuần có độ tự cảm L xác định; R = 200Ω; tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung C để điện áp hiệu dụng giữa hai đầu đoạn mạch MB đạt giá trị cực tiểu là U1 và giá trị cực đại là U2 = 400V. Giá trị của U1 là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
UMB = \(\frac{{U\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{U}{{\sqrt {\frac{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{{{R^2} + Z_C^2}}} }} = \frac{U}{{\sqrt y }}\)
với \(y = \frac{{{R^2} + {{({Z_L} - {Z_C})}^2}}}{{{R^2} + Z_C^2}}\)
\(\begin{array}{l} {y^,} = \frac{{ - 2\left( {{Z_L} - {Z_C}} \right)\left( {{R^2} + Z_C^2} \right) - 2{Z_C}\left[ {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \right]}}{{{{\left( {{R^2} + Z_C^2} \right)}^2}}}\\ \Leftrightarrow y' = \frac{{2{Z_L}\left( {Z_C^2 - {Z_L}{Z_C} - {R^2}} \right)}}{{{{\left( {{R^2} + Z_C^2} \right)}^2}}}\\ y' = \,\,khi\,\,\,{Z_C} = \frac{{{Z_L} + \sqrt {4{R^2} + Z_L^2} }}{2} \end{array}\)
Khi đó :
\(\begin{array}{l} {U_{MB\max }} = \frac{{2UR}}{{\sqrt {4{R^2} + Z_L^2} - {Z_L}}} = {U_2}\\ \frac{R}{{\sqrt {4{R^2} + Z_L^2} - {Z_L}}} = 1 \Rightarrow {\left( {R + {Z_L}} \right)^2} = 4{R^2} + Z_L^2\\ \Rightarrow {Z_L} = 1,5R\left( 1 \right) \end{array}\)
UMB = UMBmin khi ZC = 0 vì với ZC > 0 thì:
\(\begin{array}{l} \frac{{\sqrt {{R^2}} }}{{\sqrt {{R^2} + Z_L^2} }} < \frac{{\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\ {U_{MB\min }} = \frac{{U\sqrt {{R^2}} }}{{\sqrt {{R^2} + Z_L^2} }} = \frac{{UR}}{{\sqrt {{R^2} + Z_L^2} }} = {U_1}\\ {U_1} = \frac{{UR}}{{\sqrt {{R^2} + Z_L^2} }} = \frac{{UR}}{{\sqrt {{R^2} + 2,25{R^2}} }} = \frac{U}{{\sqrt {3,25} }}\\ \Leftrightarrow {U_1} = \frac{{200}}{{\sqrt {3,25} }} \approx 111V \end{array}\)
Đề thi thử tốt nghiệp THPT QG 2020 môn Vật lý
Trường THPT Thoại Ngọc Hầu



.PNG)











