Cho hình chóp S.ABCD có đáy là hình thoi cạnh , , cạnh bên và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ đến mặt phẳng ?
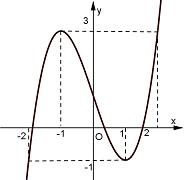
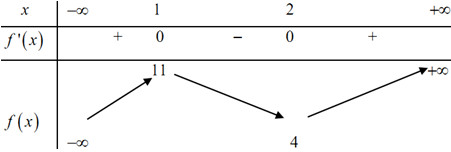
Câu 26: Cho hàm số . Tìm mệnh đề đúng trong các mệnh đề sau:
A. Hàm số nghịch biến trên các khoảng và .
B. Hàm số đồng biến trên các khoảng và .
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên .
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp giải:
- Chứng minh .
- Xác định khoảng cách từ đến .
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Lời giải chi tiết:
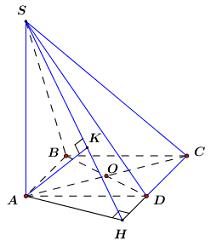
Ta có .
Trong kẻ .
Vì nên điểm nằm ngoài đoạn thẳng CD.
Trong dựng ta có:
.
.
Xét tam giác vuông AHD có , .
Vì nên , suy ra tam giác SAH vuông tại , áp dụng hệ thức lượng trong tam giác vuông ta có: .
Vậy .
Chọn A.
Đề thi giữa HK1 môn Toán 12 năm 2023 - 2024
Trường THPT Bắc Ninh



.jpg)