ADMICRO
Đồ thị hàm số có đường tiệm cận đứng là đường thẳng nào sau đây?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ZUNIA12
Lời giải:
Báo sai
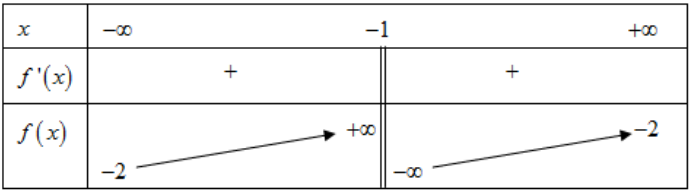
Vì và
nên
Tương tự nên đường thẳng là tiệm cận đứng của đồ thị hàm số.
ZUNIA9
AANETWORK



.PNG)











