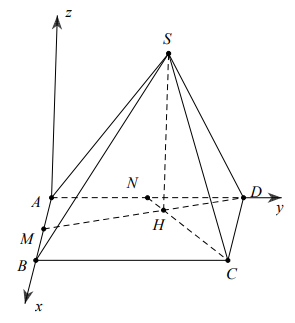
Cho hình chóp S ABCD . có đáy ABCD là hình vuông cạnh a . Gọi M và N lần lượt là trung điểm các cạnh AB và AD ; H là giao điểm của CN và DM . Biết SH vuông góc với mặt phẳng (ABCD) và \(S H=a \sqrt{3}\) . Tính khoảng cách giữa hai đường thẳng DM và SC theo a .
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn hệ trục tọa độ như hình
\(\begin{aligned} &\text { Tọa độ các đỉnh: } A(0 ; 0 ; 0), B(a ; 0 ; 0), D(0 ; a ; 0), C(a ; a ; 0), M\left(\frac{a}{2} ; 0 ; 0\right), N\left(0 ; \frac{a}{2} ; 0\right)\\ &\text { Suy ra } \overrightarrow{D M}=\left(\frac{a}{2} ;-a ; 0\right) \Rightarrow \text { phương trình } D M:\left\{\begin{array}{l} x=t \\ y=a-2 t \Rightarrow H(t ; a-2 t ; 0) \\ z=0 \end{array}\right.\\ &\Rightarrow \overrightarrow{C H}=(t-a ;-2 t ; 0), \overrightarrow{C N}=\left(-a ;-\frac{a}{2} ; 0\right)\\ &\text { Vì } H \in C N \Rightarrow \frac{t-a}{-a}=\frac{-2 t}{\frac{-a}{2}} \Leftrightarrow-t+a=4 t \Rightarrow t=\frac{a}{5} \Rightarrow H\left(\frac{a}{5} ; \frac{3 a}{5} ; 0\right) \Rightarrow S\left(\frac{a}{5} ; \frac{3 a}{5} ; a \sqrt{3}\right) \end{aligned}\)
\(\begin{array}{l} \text { Ta có: } \overrightarrow{S C}=\left(\frac{4 a}{5} ; \frac{2 a}{5} ;-a \sqrt{3}\right), \overrightarrow{D C}=(a ; 0 ; 0) \Rightarrow[\overrightarrow{D M}, \overrightarrow{S C}]=\left(a^{2} \sqrt{3} ; \frac{a^{2} \sqrt{3}}{2} ; a^{2}\right) \\ \Rightarrow[ \overrightarrow{D M}, \overrightarrow{S C}] \cdot \overrightarrow{D C}=a^{3} \sqrt{3} \\ \text { Vậy } d(S C, D M)=\frac{[ \overrightarrow{D M}, \overrightarrow{S C}] \cdot \overrightarrow{D C} \mid}{|[ \overrightarrow{D M}, \overrightarrow{S C}]|}=\frac{a^{3} \sqrt{3}}{\frac{a^{2} \sqrt{19}}{2}}=\frac{2 a \sqrt{57}}{19} \end{array}\)