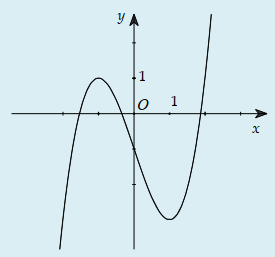
Cho hàm số y = x3-3x2+4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương trình đường thẳng d; y = k(x-1)+2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
x3-3x2+4 = k(x-1)+2.
Hay x3-3x2-kx+k+2 = 0 (1)
⇔ (x−1)(x2−2x−k−2) = 0
\( \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
\underbrace {{x^2} - 2x - k - 2}_{g\left( x \right)} = 0\left( * \right)
\end{array} \right.\)
(C) cắt d tại ba điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt x1; x2 khác 1
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\Delta {'_g} > 0}\\
{g\left( 1 \right) \ne 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{k + 3 > 0}\\
{ - 3 - k \ne 0}
\end{array} \Leftrightarrow k > - 3} \right.} \right.\)
Hơn nữa theo Viet ta có
\(\left\{ {\begin{array}{*{20}{l}}
{{x_1} + {x_2} = 2 = 2{x_I}}\\
{{y_1} + {y_2} = k\left( {{x_1} + {x_2}} \right) - 2k + 4 = 4 = 2{y_I}}
\end{array}} \right.\)
nên I là trung điểm AB.
Vậy chọn k> -3, hay k ∈ (-3; +∞).
Do đó có vô số giá trị k nguyên thỏa mãn yêu cầu bài toán.
Câu hỏi liên quan
-
Bảng biến thiên sau đây là của hàm số nào?
-
Cho đồ thị hàm số f(x) như hình bên. Hàm số nào dưới đây tương ứng với đồ thị đó?
-
Giá trị của m để phương trình \(x+\sqrt{2 x^{2}+1}=m\) có nghiệm là:
-
Hàm số \(y=\frac{2+2 x}{2+x}\) có đồ thị là hình vẽ nào sau đây?
-
Tìm số giao điểm của đồ thị (C): y = x3 + x – 2 và đường thẳng y = x – 1
-
Cho hàm số y=|x3−x|+m với m là một tham số thực. Số điểm cực trị của hàm số đã cho bằng
-
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4}-2{x^2}\) tại điểm có hoành độ x = - 2 là:
-
Tìm m để đồ thị hàm số y = x3+mx+2 cắt trục hoành tại một điểm duy nhất.
-
Bảng biến thiên ở hình dưới là của một trong bốn hàm số được liệt kê dưới đây. Hãy tìm hàm số đó
-
Biết đồ thị hàm số \( y = \frac{{2x - 1}}{{x + 3}}\) cắt trục Ox,Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB
-
Tất cả giá trị của tham số m để phương trình \({x^4} – 2{x^2} – m + 3 = 0\) có bốn nghiệm phân biệt là
-
Hàm số \(y=(x-2)(x^2-1)\)có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số \(y=|x-2|(x^2-1)\)?
-
Số giao điểm của đồ thị hàm số \(y = \left( {x – 2} \right)\left( {{x^2} + 1} \right)\) với trục hoành là
-
Cho hàm số y = f(x) xác định trên R và có đồ thị như hình bên. Hỏi phương trình f(|x-2|) = \(\frac{{ - 1}}{2}\) có bao nhiêu nghiệm?
-
Biết đồ thị (C) của hàm số y=x2−2x+3x−1 có hai điểm cực trị. Đường thẳng đi qua hai điểm cực trị của đồ thị (C) cắt trục hoành tại điểm M có hoành độ xM bằng:
-
Cho hàm số xác định, liên tục \(\mathbb{R}\) trên và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=-f(x)?
-
Cho hàm số \(y = \frac{1}{3}{x^3} + {x^2} - 2\)
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y'' = 0 là
-
Đường thẳng y = m không cắt đồ thị hàm số \(y = – 2{x^4} + 4{x^2} + 2\,\) thì tất cả các giá trị tham số m là
-
Xét một bảng ô vuông gồm 4×4 ô vuông. Người ta điền vào mỗi ô vuông một trong hai số 1 hoặc -1 sao cho tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0. Hỏi có bao nhiêu cách điền số?
-
Cho hàm số y = 2x3 - 3x2 + 1 có đồ thị và đường thẳng d: y = x - 1. Giao điểm của (C) và d lần lượt là A(1; 0); B và C. Khi đó khoảng cách giữa B và C là
