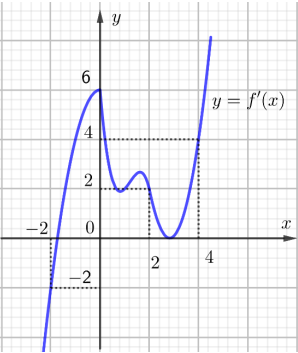
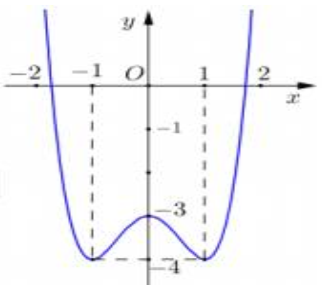
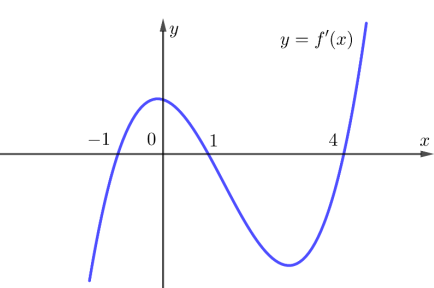
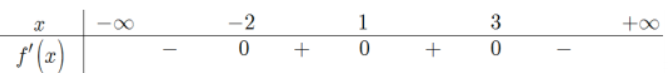Cho hàm số y =f(x)là một hàm bậc ba có bảng biến thiên
.png)
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(f\left(e^{x^{2}}\right)=m\) có đúng ba nghiệm phân biệt?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=e^{x^{2}}\) , điều kiện \(t=e^{x^{2}} \geq e^{0}=1\) . Khi đó phương trình \(f\left(e^{x^{2}}\right)=m(1)\) trở thành \(f(t)=m(2)\).
Ta có sự tương ứng giữa t và x như sau: mỗi giá trị t > 1 cho tương ứng 2 giá trị x , với t =1 thì chỉ có một giá trị tương ứng là x = 0 , với t <1 thì không cho giá trị x nào tương ứng.
Do đó phương trình (1) có 3 nghiệm phân biệt khi và chỉ khi phương trình ( 2) có 2 nghiệm phân biệt \(t_{1}, t_{2}\) thỏa mãn \(t_{1}=1<t_{2}\) , các nghiệm còn lại khác hai nghiệm trên (nếu có) thì phải bé hơn 1.
Vì phương trình (2) có một nghiệm \(t_{1}=1\) nên \(m=f(1)=1\). Khi đó dựa vào bảng biến thiên ta thấy m =1 thỏa mãn bài toán. Vậy có một giá trị nguyên của m .
Câu hỏi liên quan
-
Cho hàm số \(f(x)=m x^{4}+2 x^{2}-1 \text { với } m\) với m là tham số thực. Có tất cả bao nhiêu giá trị nguyên của m thuộc khoảng (-2020;2020) sao cho hàm số đã cho đồng biến trên khoảng \(\left(0 ; \frac{1}{2}\right) ?\)
-
Cho hàm số f(x) Hàm số y=f'(x) có đồ thị như hình sau.
.png)
Có tất cả bao nhiêu giá trị nguyên dương của tham số m đề hàm số \(g(x)=4 f(x-m)+x^{2}-2 m x+2020\) đồng biến trên khoảng (1;2).
-
Cho hàm số y = f(x) có đồ thị như hình vẽ.
Hàm số y = f(x) đồng biến trên khoảng nào sau đây?
-
Hỏi hàm số \(y\; = \;\frac{{{x^2}\; - \;3x\; + \;5}}{{x\; + \;1}}\) nghịch biến trên các khoảng nào ?
-
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng xét dấu:
Hàm số \(y=f\left(x^{2}+2 x\right)\) nghịch biến trên khoảng nào dưới đây -
Hỏi hàm số \(y=\frac{3}{5} x^{5}-3 x^{4}+4 x^{3}-2\) đồng biến trên khoảng nào?
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\frac{\cot x-1}{m \cot x-1}\) đồng biến trên khoảng \(\left(\frac{\pi}{4} ; \frac{\pi}{2}\right)\)
-
Hàm số \(y = - \frac{2}{3}{x^3} + 3{x^2} - x + 1\) nghịch biến trên khoảng nào sau đây?
-
Cho đồ thị hàm số với \(x\; \in \;\left[ { - \;\frac{\pi }{2}\;;\;\frac{{3\pi }}{2}} \right]\) như hình vẽ.
Tìm khoảng đồng biến của hàm số y = sinx với \(x\; \in \;\left[ { - \;\frac{\pi }{2}\;;\;\frac{{3\pi }}{2}} \right]\)
-
Tìm tất cả giá trị m để hàm số \(y=\frac{\sin x-m}{\sin x+m}\) nghịch biến trên \(\left(0 ; \frac{\pi}{2}\right)\).
-
Hàm số \(y = {x^2} + 2x\) đồng biến trên các khoảng:
-
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=x(x-1)^{2}(x+3), \forall x \in \mathbb{R}\) . Hàm số y=f(x) nghịch biến trên khoảng
-
Hàm số \(y = {x^3} - 2{x^2} + x - 1\) nghịch biến trên các khoảng:
-
Cho hàm số y=f(x). Đồ thị hàm y=f'(x) như hình vẽ
Đặt \(g(x)=3 f(x)-x^{3}+3 x-m\) với m là tham số thực. Điều kiện cần và đủ để bất phương trình \(g(x) \geq 0\) đúng với \(\forall x \in[-\sqrt{3} ; \sqrt{3}]\) là
-
Hàm số \(y = 2(x - 3)⁴ + 1\) đồng biến trong khoảng nào sau đây ?
-
Cho hàm số y=f(x). Đồ thị của hàm số y=f'(x) như hình vẽ bên. Đặt \(h(x)=2 f(x)-x^{2}\) . Hàm số y=h(x) đồng biến trên khoảng nào dưới đây?
-
Tìm khoảng đồng biến của hàm số \(y= 4x ³ - x ² - 4x -2\)
-
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình sau.
Tìm m để phương trình \(f\left(\mathrm{e}^{x^{2}}\right)=m^{2}+5 m\) có hai nghiệm thực phân biệt. -
Cho hàm số y=f(x). Đồ thị của hàm số y=f'(x) như hình vẽ bên. Hàm số \(y=f\left(x^{2}\right)\) đồng biến trên khoảng nào dưới đây?
-
Tìm tất cả các giá trị thực của tham số m để hàm số \(y=-x^{3}+3 x^{2}+3\left(m^{2}-1\right) x-3 m^{2}-1\) nghịch biến trên R.
