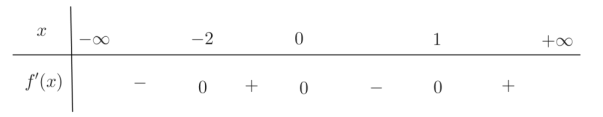Cho hàm hàm số y =f(x) có bảng biến thiên như hình vẽ dưới
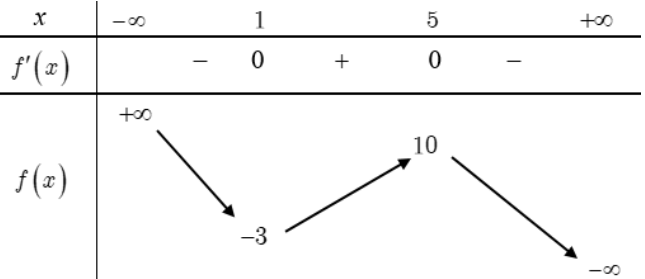
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(\left|f\left(x^{2}+1\right)\right|=m\) có 6 nghiệm phân biệt
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=x^{2}+1, t\ge 1\), từ đó phương trình trở thành \(|f(t)|=m, t \geq 1\).
Do \(t \geq 1\)nên ta xét bảng biến thiên của hàm y =f(t) trên \([1 ;+\infty)\) như sau:
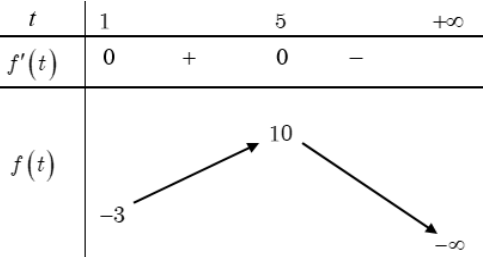
Bảng biến thiên của hàm số \(y=|f(t)|\) trên \([1 ;+\infty)\) là
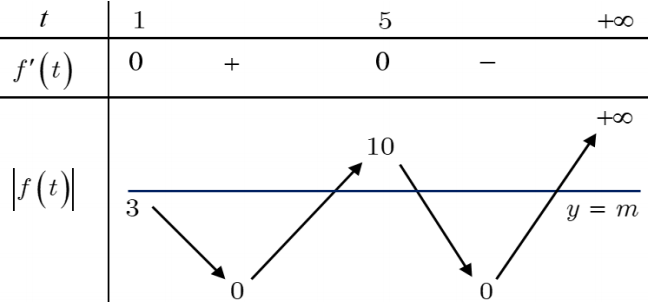
Cứ mỗi nghiệm t >1 cho được hai nghiệm x , do vậy để phương trình \(\left|f\left(x^{2}+1\right)\right|=m\) có 6 nghiệm phân biệt thì phương trình \(|f(t)|=m\) cần có 3 nghiệm t>1.
Dựa bảng biến thiên của hàm \(y=|f(t)|\) ở trên ta có điều kiện 3 <m<10 , mặt khác m nguyên nên \(m \in\{4 ; 5 ; 6 ; 7 ; 8 ; 9\}\) .
Vậy có 6 giá trị nguyên m thỏa mãn bài toán.
Câu hỏi liên quan
-
Cho hàm số \(y=|x+1|(x-2)\) Khẳng định nào sau đây là khẳng định sai?
-
Cho hàm số \(y = \frac{{\ln x – 4}}{{\ln x – 2m}}\) với m là tham số. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của S.
-
Hàm số nào dưới đây đồng biến trên \(\mathbb{R}\)?
-
Có bao nhiêu giá trị nguyên của tham số m đề hàm số \(f(x)=-x^{3}+3(m+1) x^{2}+3(2 m-1) x+2020\) nghịch biến trên tập xác định của nó?
-
Cho hàm số \(y=\frac{x}{2}+\sin ^{2} x, x \in[0 ; \pi]\) . Hỏi hàm số đồng biến trên các khoảng nào?
-
Có bao nhiêu giá trị nguyên của m để hàm số \(y=f(x)=\frac{x+2 m-3}{x-3 m+2}\) đồng biến trên \((-\infty ;-14)\).
-
Cho hàm số y =f(x) có bảng biến tiên như hình vẽ bên dưới đây. Hàm số\(y=[f(x)]^{2}-6 f(x)\) nghịch biến trên khoảng nào dưới đây
-
Tìm tất cả các giá trị thực của tham số m đề hàm số nghịch biến trên khoảng (1;+∞)
-
Hàm số nào sau đây nghịch biến trên R.
-
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y=\frac{\tan x-2}{\tan x-m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{4}\right) ?\)
-
Cho i là đơn vị ảo. Với x,y ∈ R thì x − 1 + (y + 3)i là số thuần ảo khi và chỉ khi
-
Tìm các giá trị của tham số m sao cho hàm số \(y=\frac{x+1}{x+m}\) nghịch biến trên khoảng \((2 ;+\infty) .\)
-
Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị hàm số y=f'(x) như hình vẽ.
Đặt \(g(x)=f\left(x^{2}-2\right)\) Mệnh đề nào dưới đây sai?
-
Tổng S của các giá trị m để hàm số \(y=\frac{(2 m+1) x+3}{x+m}\) nghịch biến trên (0;1) là:
-
Kết luận nào sau đây về tính đơn điệu của hàm số \(y = \frac{{2x + 1}}{{x + 1}}\) là đúng?
-
Cho hàm số \(y\; = \;\frac{{x + 1}}{{1 - x}}\) Khẳng định nào sao đây là khẳng đinh đúng?
-
Cho hàm số y = f( x).(x-1) liên tục trên R và có đồ thị như hình vẽ.
Tìm tất cả các giá trị của tham số m để phương trình f(x) : |x - 1| = m có số nghiệm lớn nhất
-
Cho hàm số y = sin2x - 2x. Hàm số này
-
Hàm số \(y=\frac{x^{3}}{3}-\frac{m x^{2}}{2}-2 x+1\) đồng biến trên tập xác định khi:
-
Cho hàm số \(y = f(x) = 2{x^3} + 6{x^2} + 6x - 2017\). Mệnh đề nào dưới đây sai
