Bộ Đề Kiểm Tra Giữa Học Kì II - Toán 10 - (Năm 2023 - 2024) - Các Trường THCS Trên Toàn Quốc - Trườhng THPT Việt Đức
Câu 1
Tập xác định của hàm số \(y = \frac{{x + 1}}{{x - 1}}\) là?
undefined.\(\mathbb{R}\backslash \left\{ { \pm 1} \right\}\)
A.\(\mathbb{R}\backslash \left\{ { - 1} \right\}\)
B.\(\mathbb{R}\backslash \left\{ 1 \right\}\)
C.\(\left( {1; + \infty } \right)\)
Câu 2
Trong các hàm số sau, hàm số nào nghịch biến trên \(\mathbb{R}\)?
undefined.\(y = x\)
A.\(y = - 2x\)
B.\(y = 2x\)
C.\(y = \frac{1}{2}x\)
Câu 3
Cho hàm số \(f\left( x \right) = \sqrt {2{x^2} + 1} \). Giá trị \(f\left( { - 2} \right)\) bằng?
undefined.\( - 3\)
A.\(3\)
B.\(4\)
C.Không xác định
Câu 4
Khoảng đồng biến của hàm số \(y = {x^2} - 4x + 3\) là?
undefined.\(\left( { - \infty ; - 2} \right)\)
A.\(\left( { - \infty ;2} \right)\)
B.\(\left( { - 2; + \infty } \right)\)
C.\(\left( {2; + \infty } \right)\)
Câu 5
Trục đối xứng của đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
undefined.\(x = - \frac{b}{{2a}}.\)
A.\(x = - \frac{c}{{2a}}.\)
B.\(x = - \frac{\Delta }{{4a}}.\)
C.\(x = \frac{b}{{2a}}\)
Câu 6
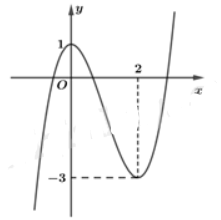
Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình vẽ dưới đây. Khẳng định nào dưới đây đúng?
undefined.\(a > 0.\)
A.\(a < 0.\)
B.\(a = 1.\)
C.\(a = 2.\)
Câu 7
Cho \(f\left( x \right) = a{x^2} + bx + c\), \(\left( {a \ne 0} \right)\) và \(\Delta = {b^2} - 4ac\). Cho biết dấu của \(\Delta \) khi \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\)?
undefined.\(\Delta < 0\)
A.\(\Delta = 0\)
B.\(\Delta > 0\)
C.\(\Delta \ge 0\)
Câu 8
Tập nghiệm \(S\) của bất phương trình \({x^2} - x - 6 \le 0\)?
undefined.\(S = \left( { - \infty ; - 3} \right) \cup \left( {2: + \infty } \right)\)
A.\(\left[ { - 2;3} \right]\)
B.\(\left[ { - 3;2} \right]\)
C.\(\left( { - \infty ; - 3} \right] \cup \left[ {2; + \infty } \right)\)
Câu 9
Tìm tập nghiệm \(S\) của bất phương trình \({x^2} - 4x + 4 > 0\)?
undefined.\(S = \mathbb{R}\backslash \left\{ 2 \right\}\)
A.\(S = \mathbb{R}\)
B.\(S = \left( {2; + \infty } \right)\)
C.\(S = \mathbb{R}\backslash \left\{ { - 2} \right\}\)
Câu 10
Phương trình \(\sqrt {x - 1} = x - 3\) có tập nghiệm là?
undefined.\(S = \left\{ 5 \right\}\)
A.\(S = \left\{ {2;5} \right\}\)
B.\(S = \left\{ 2 \right\}\)
C.\(S = \emptyset \)
Câu 11
Số nghiệm của phương trình \(\sqrt {{x^2} - 4x + 3} = \sqrt {1 - x} \) là?
undefined.Vô số
A.2
B.1
C.0
Câu 12
Trong mặt phẳng \(Oxy\), đường thẳng \(\left( d \right):\,\,ax + by + c = 0,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\). Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng \(\left( d \right)\)?
undefined.\(\overrightarrow n = \left( {a; - b} \right)\)
A.\(\overrightarrow n = \left( {b;a} \right)\)
B.\(\overrightarrow n = \left( {b; - a} \right)\)
C.\(\overrightarrow n = \left( {a;b} \right)\)
Câu 13
Phương trình tham số của đường thẳng đi qua hai điểm \(A\left( {2; - 1} \right)\) và \(B\left( {2;5} \right)\) là?
undefined.\(\left\{ \begin{array}{l}x = 2t\\y = - 6t\end{array} \right.\)
A.\(\left\{ \begin{array}{l}x = 2 + t\\y = 5 + 6t\end{array} \right.\)
B.\(\left\{ \begin{array}{l}x = 1\\y = 2 + 6t\end{array} \right.\)
C.\(\left\{ \begin{array}{l}x = 2\\y = - 1 + 6t\end{array} \right.\)
Câu 14
Trong mặt phẳng \(Oxy\), đường thẳng \(d:\,x - 2y - 1 = 0\) song song với đường thẳng có phương trình nào sau đây?
undefined.\(x + 2y + 1 = 0\)
A.\(2x - y = 0\)
B.\( - x + 2y + 1 = 0\)
C.\( - 2x + 4y - 1 = 0\)
Câu 15
Tính góc giữa hai đường thẳng \(\Delta :x - \sqrt 3 y + 2 = 0\) và \(\Delta ':x + \sqrt 3 y - 1 = 0\)?
undefined.\({90^ \circ }\)
A.\({120^ \circ }\)
B.\({60^ \circ }\)
C.\({30^ \circ }\)
Câu 16
Khoảng cách từ điểm \(M\left( {5\,;\, - 1} \right)\) đến đường thẳng \(3x + 2y + 13 = 0\) là?
undefined.\(2\sqrt {13} \)
A.\(\frac{{28}}{{\sqrt {13} }}\)
B.\(26\)
C.\(\frac{{\sqrt {13} }}{2}\)
Câu 17
Phương trình nào sau đây là phương trình đường tròn?
undefined.\({x^2} + {y^2} - 6x - 10y + 30 = 0\)
A.\({x^2} + {y^2} - 3x - 2y + 30 = 0\)
B.\(4{x^2} + {y^2} - 10x - 6y - 2 = 0\)
C.\({x^2} + 2{y^2} - 4x - 8y + 1 = 0\)
Câu 18
Phương trình nào sau đây là phương trình của đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính bằng \(3\)?
undefined.\({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\)
A.\({\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\)
B.\({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\)
C.\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 9\)
Câu 19
Đường elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{7} = 1\) cắt trục tung tại hai điểm \({B_1}\), \({B_2}\). Độ dài \({B_1}{B_2}\) bằng?
undefined.\(\sqrt 7 \)
A.\(2\sqrt 7 \)
B.\(3\)
C.\(6\)
Câu 20
Tọa độ các tiêu điểm của hypebol \(\left( H \right):\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\) là?
undefined.\({F_1} = \left( { - 5;0} \right);{F_2} = \left( {5;0} \right)\)
A.\({F_1} = \left( {0; - 5} \right);{F_2} = \left( {0;5} \right)\)
B.\({F_1} = \left( {0; - \sqrt 7 } \right);{F_2} = \left( {0;\sqrt 7 } \right)\)
C.\({F_1} = \left( { - \sqrt 7 ;0} \right);{F_2} = \left( {\sqrt 7 ;0} \right)\)
Câu 21
Tập xác định của hàm số \(y = \sqrt {4 - x} + \sqrt {x - 2} \) là?
undefined.\(D = \left( {2;4} \right)\)
A.\(D = \left[ {2;4} \right]\)
B.\(D = \left\{ {2;4} \right\}\)
C.\(D = \left( { - \infty ;2} \right) \cup \left( {4; + \infty } \right)\)
Câu 22
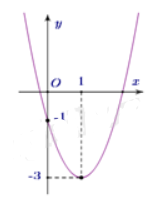
Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
undefined.Hàm số nghịch biến trên khoảng \(\left( {0;3} \right)\)
A.Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\)
B.Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\)
C.Hàm số đồng biến trên khoảng \(\left( { - \infty ;3} \right)\)
Câu 23
Đồ thị hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}2x + 3{\rm{ }}\,\,\,khi{\rm{ }}x \le 2\\{x^2} - 3{\rm{ }}\,\,\,khi{\rm{ }}x > 2\end{array} \right.\) đi qua điểm có tọa độ nào sau đây?
undefined.\(\left( {0; - 3} \right)\)
A.\(\left( {3;6} \right)\)
B.\(\left( {2;5} \right)\)
C.\(\left( {2;1} \right)\)
Câu 24
Cho parabol \(y = a{x^2} + bx + c\) có đồ thị như hình:
Phương trình của parabol này là?
undefined.\(y = - {x^2} + x - 1\)
A.\(y = 2{x^2} + 4x - 1\)
B.\(y = {x^2} - 2x - 1\)
C.\(y = 2{x^2} - 4x - 1\)
Câu 25
Tọa độ giao điểm của \(\left( P \right)\,:\,y = {x^2} - 4x\) với đường thẳng \(d\,:\,y = - x - 2\) là?
undefined.\(M\left( {0;\, - 2} \right)\), \(N\left( {2;\, - 4} \right)\)
A.\(M\left( { - 1;\, - 1} \right)\), \(N\left( { - 2;\,0} \right)\)
B.\(M\left( {\, - 3;\,1} \right)\), \(N\left( {3;\, - 5} \right)\)
C.\(M\left( {1;\, - 3} \right)\), \(N\left( {2;\, - 4} \right)\)
Câu 27
Tìm tất cả các giá trị của tham số \(m\) để bất phương trình \({x^2} - \left( {m + 2} \right)x + 8m + 1 \le 0\) vô nghiệm?
undefined.\(m \in \left[ {0;28} \right]\)
A.\(m \in \left( { - \infty ;0} \right) \cup \left( {28; + \infty } \right)\)
B.\(m \in \left( { - \infty ;0} \right] \cup \left[ {28; + \infty } \right)\)
C.\(m \in \left( {0;28} \right)\)
Câu 29
Cho đường thẳng \(d\) có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng \(d\) là?
undefined.\(2x + y - 1 = 0\)
A.\( - 2x + y - 1 = 0\)
B.\(x + 2y + 1 = 0\)
C.\(2x + 3y - 1 = 0\)
Câu 30
Đường thẳng \(d\) đi qua điểm \(M\left( { - 2;1} \right)\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + 5t\end{array} \right.\) có phương trình tham số là?
undefined.\(\left\{ \begin{array}{l}x = - 2 - 3t\\y = 1 + 5t\end{array} \right..\)
A.\(\left\{ \begin{array}{l}x = - 2 + 5t\\y = 1 + 3t\end{array} \right..\)
B.\(\left\{ \begin{array}{l}x = 1 - 3t\\y = 2 + 5t\end{array} \right..\)
C.\(\left\{ \begin{array}{l}x = 1 + 5t\\y = 2 + 3t\end{array} \right..\)
Câu 31
Tìm tất cả các giá trị của tham số \(m\) để khoảng cách từ điểm \(A\left( { - 1;2} \right)\) đến đường thẳng \(\Delta :mx + y - m + 4 = 0\) bằng \(2\sqrt 5 \)?
undefined.\(m = 2.\)
A.\(\left[ \begin{array}{l}m = - 2\\m = \frac{1}{2}\end{array} \right.\)
B.\(m = - \frac{1}{2}\)
C.Không tồn tại \(m\)
Câu 32
Trong mặt phẳng \(Oxy\), đường tròn đi qua ba điểm \(A\left( {1;2} \right)\), \(B\left( {5;2} \right)\), \(C\left( {1; - 3} \right)\) có phương trình là?
undefined.\({x^2} + {y^2} + 25x + 19y - 49 = 0\)
A.\(2{x^2} + {y^2} - 6x + y - 3 = 0\)
B.\({x^2} + {y^2} - 6x + y - 1 = 0\)
C.\({x^2} + {y^2} - 6x + xy - 1 = 0\)
Câu 33
Trong hệ trục tọa độ \(Oxy\), cho đường tròn \(\left( C \right)\) đi qua hai điểm \(A\left( {1;\,2} \right),\,B\left( {3,\,4} \right)\) và tiếp xúc với đường thẳng \(\Delta :\,3x + y - 3 = 0\), biết tâm của \(\left( C \right)\) có tọa độ là những số nguyên. Phương trình đường tròn \(\left( C \right)\) là?
undefined.\({x^2} + {y^2} - 3x - 7y + 12 = 0.\)
A.\({x^2} + {y^2} - 6x - 4y + 5 = 0.\)
B.\({x^2} + {y^2} - 8x - 2y + 7 = 0.\)
C.\({x^2} + {y^2} - 2x - 8y + 20 = 0.\)
Câu 34
Cho đường hypebol có phương trình \(\left( H \right):100{x^2} - 25{y^2} = 100\). Tiêu cự của hypebol đó là?
undefined.\(2\sqrt {10} \)
A.\(2\sqrt {104} \)
B.\(\sqrt {10} \)
C.\(\sqrt {104} \)
Câu 35
Cho parabol \(\left( P \right):{y^2} = 8x\) có tiêu điểm là?
undefined.\(F\left( {0;4} \right)\)
A.\(F\left( {0;2} \right)\)
B.\(F\left( {2;0} \right)\)
C.\(F\left( {4;0} \right)\)
Câu 36
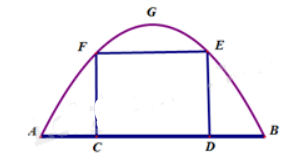
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ. Biết chiều cao cổng parabol là 4m còn kích thước cửa ở giữa là 3m x 4m. Hãy tính khoảng cách giữa hai điểm A và B?
undefined.\(AB = 4\)
A.\(AB = 2\)
B.\(AB = 8\)
C.\(AB = 6\)
Câu 37
Cho Parapol\(\left( P \right):{y^2} = 2px\,\left( {p > 0} \right)\). Chọn mệnh đề đúng trong các mệnh đề sau?
undefined.\(\left( P \right)\) có tiêu điểm \(F\left( {0\,;\,\frac{p}{2}} \right).\)
A.\(\left( P \right)\) có tiêu điểm \(F\left( { - \frac{p}{2}\,;\,0} \right).\)
B.\(\left( P \right)\) có phương trình đường chuẩn \(\Delta :y = \frac{p}{2}.\)
C.\(\left( P \right)\) có phương trình đường chuẩn \(\Delta :x = - \frac{p}{2}.\)
Câu 38
Phương trình \(\sqrt {{x^2} + 2x - 3} = 5 - x\) có nghiệm là \(x = \frac{a}{b}\). Khi đó \(a + 2b\) bằng?
undefined.\(10\)
A.\(13\)
B.\(33\)
C.\(17\)
Câu 39
Trong mặt phẳng \(Oxy,\) gọi S là tập hợp tất cả các giá trị của tham số m để góc giữa hai đường thẳng \(d:mx + \left( {m - 1} \right)y + 2 = 0\) và \(\Delta :x - y + 2 = 0\) bằng \(30^\circ .\) Tích tất cả các phần tử của tập S bằng?
undefined.\(1\)
A.\( - \frac{1}{6}\)
B.\(\frac{1}{6}\)
C.\( - 1\)
Top 10/0 lượt thi
| Tên | Điểm | Thời gian |
|---|