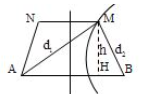
Tại mặt nước có hai nguồn sóng (A, B ) giống hệt nhau cách nhau (8cm ), gọi (M, N ) là hai điểm trên mặt nước sao cho (MN = 4cm ) và tạo với (AB )một hình thang cân (( (MN//AB) ) ), biết (M,N ) dao động với biên độ cực đại. Bước sóng trên mặt nước là (1cm ). Để trên đoạn (MN ) có đúng (5 ) điểm dao động cực đại thì diện tích của hình thang phải là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Để trên đoạn MN có 5 cực đại thì M phải thuộc cực đại bậc 2 nên k=2
M là cực đại thì \( {{\rm{d}}_1} - {d_2} = k\lambda = 2.1 = 2cm(1)\)
Xét tam giác AHMcó:
\( d_1^2 = A{M^2} = A{H^2} + H{M^2} = {(AO + OH)^2} + {h^2} = {\left( {\frac{{AB}}{2} + OH} \right)^2} + {h^2} = {6^2} + {h^2}\left( 2 \right)\)
Tương tự xét tam giác BMH có:
\( d_2^2 = B{M^2} = B{H^2} + H{M^2} = {\left( {OB - OH} \right)^2} + {h^2} = {\left( {\frac{{AB}}{2} - OH} \right)^2} + {h^2} = {2^2} + {h^2}\left( 3 \right)\)
Lấy (2) trừ (3) vế theo vế ta có: \( {\rm{d}}_1^2 - d_2^2 = 32\left( 4 \right)\) từ (1) thay vào (4) suy ra:
\( \left( {{d_1} - {d_2}} \right)\left( {{d_1} + {d_2}} \right) = 32 \Rightarrow {d_1} + {d_2} = \frac{{32}}{{{d_1} - {d_2}}} = \frac{{32}}{2} = 16cm\)
Vậy ta có hệ: \(\left\{ \begin{array}{l} {d_1} - {d_2} = 2\\ {d_1} + {d_2} = 16 \end{array} \right. \to \left\{ \begin{array}{l} {d_1} = 9cm\\ {d_2} = 7cm \end{array} \right.\)
Thay vào (2) suy ra: \(h=3\sqrt5cm\)
Vậy diện tích lớn nhất của hình thang: \(S = \frac{1}{2}.h\left( {AB + MN} \right) = 18\sqrt 5 c{m^2}\)
Câu hỏi liên quan
-
Phát biểu nào sau đây về sóng cơ là không đúng?
-
Khi nói về các đại lượng đặc trưng của sóng cơ học, phát biểu nào sau đây là sai?
-
Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm t_0 một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử M và O dao động lệch pha nhau?
-
Để khảo sát giao thoa sóng cơ, người ta bố trí trên mặt nước nằm ngang hai nguồn kết hợp S1 và S2. Hai nguồn này dao động điều hòa theo phương thẳng đứng, cùng pha. Xem biên độ sóng không thay đổi trong quá trình truyền sóng. Các điểm thuộc mặt nước và nằm trên đường trung trực của đoạn S1S2 sẽ
-
Một sóng hình sin truyền dọc theo một dây dài khoảng thời gian ngắn nhất để cho một phần tử của dây chuyển động từ vị trí biên về vị trí cân bằng là 0,17s. Nếu bước sóng bằng 1,4m thì tốc độ của sóng là bao nhiêu?
-
Một sóng có tần số 120 Hz truyền trong một môi trường với tốc độ 60 m/s thì bước sóng của nó bằng bao nhiêu?
-
Trên mặt một chất lỏng, tại O có một nguồn sóng cơ dao động có tần số f = 30 Hz. Vận tốc truyền sóng là một giá trị nào đó trong khoảng \(1,6\text{ m/s}<v<2,9\text{ m/s}.\) Biết tại điểm M cách O một khoảng 10 cm sóng tại đó luôn dao động ngược pha với dao động tại O. Giá trị của vận tốc đó là
-
Điều nào sau đây đúng khi nói về bước sóng?
-
Một dây đàn hồi rất dài có đầu A dao động với tần số f theo phương vuông góc với sợi dây. Biên độ dao động là a, vận tốc truyền sóng trên dây là 4 m/s. Xét điểm M trên dây và cách A một đoạn 14 cm, người ta thấy M luôn dao động ngược pha với A. Biết tần số f có giá trị trong khoảng từ 98 Hz đến 102 Hz. Bước sóng có giá trị là
-
Bước sóng là khoảng cách giữa hai điểm
-
Sóng ngang là sóng có phương dao động
-
Một con dơi đang bay với tốc độ 9 km/h thì phát ra sóng siêu âm có tần số 50000 Hz. Sóng siêu âm này gặp vật cản đang đứng yên phía trước và truyền ngược lại. Biết tốc độ truyền âm trong không khí là 330 m/s. Tính tần số sóng siêu âm phản xạ mà con dơi nhận được
-
Một nguồn sóng cơ dao động điều hoà theo phương trình: \(u=Acos\left( 5\pi t+\frac{\pi }{2} \right)\,\,\left( cm \right).\) Trong đó t đo bằng giây. Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng mà pha dao động lệch nhau \(\frac{3\pi }{2}\) là 0,75 m. Bước sóng và tốc độ truyền sóng lần lượt là
-
Một sóng cơ học truyền dọc theo trục Ox với phương trình \(u = 5cos\left( {8\pi t--0,04\pi x} \right)\) (u và x tính bằng cm, t tính bằng s). Tại thời điểm t = 3 s, ở điểm có x = 25 cm, phần tử sóng có li độ là
-
Biểu thức nào sau đây xác định tần số mà máy thu ghi nhận được khi nguồn âm chuyển động ra xa máy thu đứng yên
-
Một sóng cơ có tần số f, truyền trên dây đàn hồi với tốc độ truyền sóng v và bước sóng Hệ thức đúng là
-
Tạo sóng ngang tại O trên một dây đàn hồi. Điểm M cách nguồn phát sóng O một khoảng d = 20 cm có phương trình dao động \({{u}_{M}}=5cos2\pi \left( t-0,125 \right)\text{ }cm.\) Vận tốc truyền sóng trên dây là 80 cm/s. Phương trình dao động của nguồn O là phương trình dao động trong các phương trình sau?
-
Phương trình \(u=Acos\left( 0,4\pi x+7\pi t\text{ }+\frac{\pi }{3} \right)\) (x tính bằng mét, t tính bằng giây) biểu diễn một sóng truyền dọc theo trục Ox với vận tốc
-
Ở mặt nước, tại hai điểm A và B cách nhau 24cm có hai nguồn sóng kết hợp dao động theo phương thẳng đứng với cùng phương trình u=5cos20πt(mm) (t tính bằng s). Ở mặt nước, gọi I là điểm cách đều A và B một đoạn 13cm, (C) là đường tròn tâm I bán kính 4cm, M là điểm thuộc (C). Biết tại MM có các phần tử dao động với biên độ cực đại và cách xa A nhất. Tốc độ sóng truyền trên mặt nước là 40cm/s. M nằm trên đường cực đại giao thoa bậc
-
Hai sóng dao động cùng pha khi độ lệch pha của hai sóng ∆φ bằng
