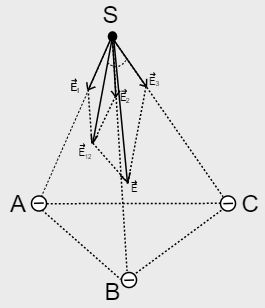
Tại 3 đỉnh ABC của tứ diện đều SABC cạnh a trong chân không có ba điện tích điểm q giống nhau (q<0).Xác định điện trường tại đỉnh S của tứ diện.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi \( \overrightarrow {{E_1}} ,\overrightarrow {{E_2}} ,\overrightarrow {{E_3}} \) là các vectơ cường độ điện trường do các điện tích q tại ba đỉnh A,B,C gây ra tại đỉnh S của tứ diện.
Ta có \( {E_1} = {E_2} = {E_3} = k.\frac{{\left| q \right|}}{{S{A^2}}} = k.\frac{{\left| q \right|}}{{{a^2}}}\)
Từ hình vẽ:
\(\begin{array}{l} \left( {\widehat {\overrightarrow {{E_1}} ,\overrightarrow {{E_2}} }} \right) = \widehat {ASB} = {60^o}\\ \overrightarrow {{E_{12}}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \Rightarrow E_{12}^2 = 2E_1^2\left( {1 + cos{{60}^o}} \right) = 3E_1^2\\ \left( {\widehat {\overrightarrow {{E_{12}}} ,\overrightarrow {{E_3}} }} \right) = \left( {\widehat {SC,\left( {SAB} \right)}} \right) = \alpha \end{array}\)
Gọi H là hình chiếu của C xuống mặt phẳng SAB, M là hình chiếu của S xuống đoạn AB.
\(\begin{array}{l} \Rightarrow SH = \frac{2}{3}SM = \frac{2}{3}\sqrt {S{A^2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\\ cos\alpha = \frac{{SH}}{{SC}} = \frac{{\frac{{a\sqrt 3 }}{3}}}{a} = \frac{{\sqrt 3 }}{3}\\ \Rightarrow \vec E = \overrightarrow {{E_{12}}} + \overrightarrow {{E_3}} \Rightarrow {E^2} = E_{12}^2 + E_3^2 + 2{E_{12}}.{E_3}.cos\alpha = 3E_1^2 + E_1^2 + 2.\sqrt 3 {E_1}.{E_1}.\frac{{\sqrt 3 }}{3} = 6E_1^2\\ \Rightarrow E = \sqrt 6 {E_1} = \sqrt 6 .k.\frac{{\left| q \right|}}{{{a^2}}} \end{array}\)
Câu hỏi liên quan
-
Ở bán dẫn loại n thì
-
Chọn phát biểu đúng về chất khí ?
-
Sự phóng điện thành miền, nếu giảm áp suất rất thấp cỡ 10-3 mmHg thì có hiện tượng gì?
-
Tìm phát biểu sai
-
Sự phóng điện thành miền của chất khí xảy ra trong các điều kiện nào
-
Quá trình dẫn điện nào dưới đây của chất khí là quá trình dẫn điện không tự lực ?
-
Phát biểu nào sau đây là đúng?
-
Chất khí có thể dẫn điện không cần tác nhân ion hóa trong điều kiện
-
Để có thể tạo ra sự phóng tia lửa điện giữa hai điện cực đặt trong không khí ở điều kiện thường thì
-
Các hiện tượng: tia lửa điện, sét, hồ quang điện, hiện tượng nào là quá trình phóng điện tự lực ?
-
Dòng điện trong môi trường nào dưới đây là dòng chuyển dời có hướng của các ion dương, ion âm và êlectron?
-
Nguyên nhân gây ra hiện tượng toả nhiệt trong dây dẫn khi có dòng điện chạy qua là:
-
Trong các cách dưới đây, cách nào dưới đây tạo ra tia lửa điện ?
-
Nguyên nhân của hiện tượng nhân hạt tải điện là
-
Nhận xét nào sau đây sai đối với đường vôn - ampe của chất khí?
-
Dòng điện trong chất khí là dòng chuyển dời có hướng của:
-
Trong các dòng điện sau đây:
I. Dòng điện qua dây dẫn kim loại (nhiệt độ không thay đổi)
II. Dòng điện qua bình điện phân có dương cực tan
III. Dòng điện trong chất khí
Dòng điện nào tuân theo định luật Ôm?
-
Cơ chế nào sau đây không phải là cách tải điện trong quá trình dẫn điện tự lực ở chất khí?
-
Hiện tượng nào sau đây có sự phát xạ nhiệt electron ?
-
Các hiện tượng: tia lửa điện, sét, hồ quang điện, hiện tượng nào xảy ra do tác dụng của điện trường rất mạnh trên 106V/m
