Một sóng cơ truyền dọc theo một sợi dây đàn hồi rất dài với biên độ 6 mm. Tại một thời điểm, hai phần tử trên dây cùng lệch khỏi vị trí cân bằng 3 mm, chuyển động ngược chiều với độ lớn vận tốc \(0,3π \sqrt3cm/s\) và cách nhau một khoảng ngắn nhất là 8cm (tính theo phương truyền sóng). Tốc độ truyền sóng trên dây là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
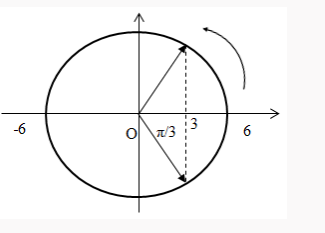
Báo saiTại một thời điểm, hai phần tử trên dây cùng lệch khỏi vị trí cân bằng 3mm, chuyển động ngược chiều với độ lớn vận tốc \(0,3π \sqrt3cm/s\) và cách nhau một khoảng ngắn nhất 8cm. Biểu diễn trên đường tròn lượng giác:
Từ đường tròn lượng giác, xác định được độ lệch pha của hai phần tử trên dây:
\( {\rm{\Delta }}\varphi = \frac{{2\pi }}{3} \Rightarrow \frac{{2\pi }}{3} = \frac{{2\pi {d_{\min }}}}{\lambda } \Rightarrow \lambda = 3{d_{\min }} = 3.8 = 24cm\)
Sử dụng hệ thức độc lập theo thời gian của x và v ta có:
\( {A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \Rightarrow \omega = \frac{v}{{\sqrt {{A^2} - {x^2}} }} = \frac{{3\pi \sqrt 3 }}{{\sqrt {{6^2} - {3^2}} }} = \pi \left( {rad/s} \right) \Rightarrow f = \frac{\omega }{{2\pi }} = 0,5Hz\)
Tốc độ truyền sóng trên dây:\( v = λ.f = 24.0,5 = 12 cm/s\)