Một nhà địa chất học đang ở tại điểm \(A\) trên sa mạc. Anh ta muốn đến điểm \(B\) và cách \(A\) một đoạn là 70 km. Trong sa mạc thì xe anh ta chỉ có thể di chuyển với vận tốc là \(30\text{km}/\text{h}\). Nhà địa chất phải đến được điểm \(B\) sau 2 giờ. Vì vậy, nếu anh ta đi từ \(A\) đến \(B\) sẽ không thể đến đúng giờ được. May mắn thay, có một con đường nhựa song song với đường nối \(A\) và \(B\) và cách AB một đoạn 10 km. Trên đường nhựa đó thì xe nhà địa chất này có thể di chuyển với vận tốc \(50\text{km}/\text{h}\). Thời gian ngắn nhật đề nhà địa chất di chuyển từ \(A\) đến \(B\) là bao nhiêu phút?

Ông Toàn có một mảnh đất phẳng hình elip có độ dài trục lớn bằng \({16}\) m và độ dài trục nhỏ là \({10}\) m. Ông để một dải đất rộng \({8}\) m làm sân, lối đi và dải đất này nhận trục bé của elip làm trục đối xứng đồng thời ông muốn trồnghoa hai bên mảnh đất còn lại. Biết kinh phí để trồng hoa là \({100\,000}\) đồng/m\({^2}\). Hỏi ông Toàn cần bao nhiêu triệu đồng trồng hoa trên phần đất đó (kết quả được làm tròn đến hàng trăm)?

Một người đàn ông muốn chèo thuyền ở vị trí \(A\) tới điểm \(B\) về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng \(3\,\,\text{km}\) (như hình vẽ).

Anh có thể chèo thuyền của mình trực tiếp qua sông để đến \(C\) và sau đó chạy đến \(B\), hay có thể chèo trực tiếp đến \(B\), hoặc anh ta có thể chèo thuyền đến một điểm \(D\) giữa \(C\) và \(B\) và sau đó chạy đến \(B\). Biết anh ấy có thể chèo thuyền \(6\,\,\text{km/}\,\text{h}\), chạy \(8\,\,\text{km/}\,\text{h}\) và quãng đường \(BC=8\,\,\text{km}\). Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Gọi \(x\,\,\left( \text{km} \right)\) là độ dài quãng đường \(BD\). Xét tính đúng sai trong các khẳng định sau:

Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất \(8000\) quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất \(30\) quả bóng trong một giờ. Chi phí thiết lập các máy này là \(200\) nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là \(192\) nghìn đồng một giờ. Số máy móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động là thấp nhất?

Một người cần xây một nhà kho có mặt tiền mở và sàn hình vuông và có thể tích là \(10000\,{{m}^{3}}\) Biết chi phí thi công sàn là 500 ngàn đồng/\({{m}^{2}}\),  chi phí thi công vách là 800 ngàn đồng/\({{m}^{2}}\),  chi phí thi công phần mái là 1 triệu đồng/\({{m}^{2}}\) Biết tổng chi phí chi phí thi công nhà kho là thấp nhất, khi đó diện tích sàn nhà kho bằng bao nhiêu mét vuông?

Trong một bài thực hành huấn luyện quân sự có một tình huống chiến sĩ phải bơi qua sông để tấn công mục tiêu ở ngay phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi của chiến sĩ bằng một phần ba vận tốc chạy trên bộ. Biết dòng sông là thẳng, mục tiêu cách chiến sỹ 1km theo đường chim bay và chiến sỹ cách bờ bên kia 100m. Hãy cho biết chiến sỹ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất (làm tròn kết quả đến hàng đơn vị)?

Giả sử cường độ ánh sáng của một nguồn điểm tỉ lệ thuận với cường độ của nguồn sáng đó và tỉ lệ nghịch với bình phương khoảng cách từ điểm đó đến nguồn sáng. Hai nguồn điểm có cường độ lần lượt là \(S\) và \(8S\), cách nhau 90 cm. Xét một điểm \(M\) nằm trên đoạn thẳng nối hai nguồn, cường độ ánh sáng tại điểm đó nhỏ nhất thì điểm đó cách nguồn có cường độ \(S\) bằng bao nhiêu centimet? (cho biết cường độ sáng tại điểm \(M\) bằng tổng cường độ sáng mỗi nguồn tại điểm đó).

Nhà máy A chuyên sản xuất một loại sản phẩm cho nhà máy Hai nhà máy thỏa thuận rằng, hằng tháng A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 tấn sản phẩm). Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi sản phẩm là \(P\left( x \right)=45-0,001{{x}^{2}}\) (triệu đồng). Chi phí để A sản xuất x tấn sản phẩm trong một tháng là \(C\left( x \right)=100+30x\) triệu đồng (gồm 100 triệu đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm). Nhà máy A bán cho B bao nhiêu tấn sản phẩm để lợi nhuận thu được là lớn nhất? (làm tròn kết quả đến hàng phần mười).

Một nguời bình thường với chiều cao \(h\text{ }\!\!~\!\!\text{ cm}\), nặng \(w\) kilogram có diện tích bề mặt cơ thể \(S\) được mô hình hoá bởi công thức \(S=\frac{1}{60}\cdot {{w}^{0.5}}\cdot {{h}^{0.5}}\) (\({{\text{m}}^{2}}\)) (công thức Mosteller). Một đối tượng có chiều cao bằng 168 cm, nặng 62 kg tham gia một cuộc nghiên cứu về sức khỏe trong 5 năm. Người ta nhận thấy cân nặng của đối tượng quan sát thay đổi với tốc độ \({w}'\left( t \right)=0,02{{t}^{2}}+0,2t\text{ }\!\!~\!\!\text{ kg}/\) năm \(\left( 0\le t\le 5 \right)\) và chiều cao tăng đều mỗi năm \(0,5\text{ }\!\!~\!\!\text{ cm}\). Sau 5 năm quan sát, diện tích bề mặt cơ thề của đối tượng trên tăng thêm bao nhiêu centimet vuông so với ban đầu? (làm tròn kết quả đến hàng đơn vi).

Một căn nhà bỏ hoang có dạng hình lập phương cạnh bằng 5m có 3 chú nhện sinh sống. Mùa đông đến, vì đói rét nên chúng đành quyết định hợp tác với nhau giăng lưới để bắt mồi. Ba chú nhện tính toán sẽ giăng một mảnh lưới hình tam giác theo cách sau: Mỗi chú nhện sẽ đứng ở mép tường bất kỳ ( có thể mép giữa 2 bức tường,giữa tường với trần nhà, hoặc giữa tường với với nền), rồi phóng những sợi tơ làm khung đến vị trí của 2 con nhện còn lại rồi sau đó mới phóng tơ dính đan phần lưới bên trong. Chúng quy định không có bất kỳ 2 con nhện nào nằm cùng trên một mặt tường, nền hoặc trần nhà. Chu vi nhỏ nhất của mảnh lưới ấy (các sợi tơ khung căn và không chùm) là \(\frac{m\sqrt{n}}{p}\) (với \(m,n,p\in {{\mathbb{N}}^{*}}\)) và \(\frac{m}{p}\) là phân số tối giản. Tính giá trị của biểu thức \(m+n+p\) ?

Một công ty vận tải cần giao hàng đến tất cả các thành phố A, B, C, D, E (hình vẽ bên dưới). Chi phí di chuyển giữa các thành phố được mô tả trên hình. Xe giao hàng của công ty xuất phát từ một thành phố trong năm thành phố trên đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố ban đầu. Tìm chi phí thấp nhất của xe giao hàng.

Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là \(2,25\) mét, chiều rộng tiếp giáp với mặt đất là \(3\) mét. Giá thuê mỗi mét vuông là \(150000\) đồng. Vậy số tiền bác Năm phải trả là bao nhiêu?

Nhà máy A chuyên sản xuất một loại sản phẩm cho nhà máy Hai nhà máy thỏa thuận rằng, hằng tháng A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B (tối đa 100 tấn sản phẩm). Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là \(P\left( x \right)=45-0,001{{x}^{2}}\) (triệu đồng). Chi phí để A sản xuất x tấn sản phẩm trong một tháng là \(C\left( x \right)=100+30x\) triệu đồng (gồm 100 triệu đồng chi phí cố định và 30 triệu đồng cho mỗi tấn sản phẩm). Hỏi Nhà máy B đặt đơn hàng bao nhiêu tấn thì nhà máy A thu được lợi nhuận lớn nhất? (làm tròn kết quả đến hàng phần mười).

Nhà máy \(A\) chuyên sản xuất một loại sản phẩm cho nhà máy \(B\). Hai nhà máy thỏa thuận rằng, hằng tháng \(A\) cung cấp cho \(B\) số lượng sản phẩm theo đơn đặt hàng của \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(X\) tấn sản phẩm thì giá bán cho mỗi sản phẩm là \(P\left( x \right)=45-0,001{{x}^{2}}\) (triệu đồng). Chi phí để \(A\) sản xuất x tấn sản phẩm trong một tháng là \(C\left( x \right)=100+30x\) triệu đồng (gồm \(100\) triệu đồng chi phí cố định và \(30\) triệu đồng cho mỗi tấn sản phẩm). Nhà máy\(A\) bán cho \(B\) bao nhiêu tấn sản phẩm để lợi nhuận thu được là lớn nhất? (làm tròn kết quả đến hàng phần mười).

Một con cá hồi bơi ngược dòng (từ nơi sinh sống) vượt khoảng cách 300 km để tới nơi sinh sản. Vận tốc dòng nước là \(6\text{ }\!\!~\!\!\text{ km}/\text{h}\). Giả sử vận tốc hơi của cả khi mước đứng yên là \(v\text{ }\!\!~\!\!\text{ km}/\text{h}\) thì năng lượng tiêu hao của cả trong \(t\) giờ cho bởi công thức \(E\left( v \right)=c{{v}^{3}}t\) trong đó \(c\) là hàng số cho trước. \(E\) tính hằng Jun. Tính vận tốc bơi của cả khi nước đứng yên, để năng lượng của cả tiêu hao ít nhất?

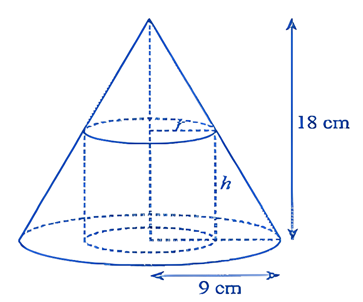
Trong hình bên cho biết một hình trụ bán kính đáy \(r\left( cm \right)\), chiều cao \(h\left( cm \right)\) nội tiếp hình nón có bán kính đáy \(9\,cm\), chiều cao \(18\,cm\). Tìm giá trị của \(r\) để thể tích của hình trụ là lớn nhất. (kết quả làm tròn đến hàng đơn vị của \(cm\))

Một nhà máy sản xuất \(\text{ }x\) sản phẩm trong mỗi tháng. Chi phí sản xuất \(x\) sản phẩm được cho bởi hàm chi phí

\(C\left( x \right)=16\,000+500x-1,6{{x}^{2}}+0,004{{x}^{3}}\) (nghìn đồng).

Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm \(x\) và được cho bởi công thức \(p\left( x \right)=1700-7x\) (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.

Một ông chủ nhà muốn làm một cái thang cứu hộ khi có nguy hiểm xảy ra. Ông ta muốn làm cái thang để nó đứng dưới đất vươn qua hàng rào tựa vào ngôi nhà. Với hàng rào cao 2,4 mét được đặt song song và cách bức tường của ngôi nhà một khoảng bằng 1,5 mét. Chiều dài ngắn nhất của cây thang bao nhiêu mét để nó đứng dưới đất vươn qua hàng rào tựa vào ngôi nhà (tham khảo hình vẽ) (làm tròn đến chữ số thập phân thứ 2)?

Trong lớp học, màn hình tivi hình chữ nhật có chiều cao 1m được đặt ở độ cao \(1,2m\) so với tầm mắt của học sinh (tính từ đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí ngồi sao cho góc nhìn lớn nhất (\(\widehat{BOC}\) là góc nhìn). 

Nếu xét học sinh Nam ngồi nhìn thẳng màn hình thì học sinh Nam ngồi bàn thứ mấy nhìn được rõ nhất, biết vị trí ngồi bàn đầu tiên cách tivi \(1,2m\) và mỗi bàn kế tiếp nhau cách nhau \(0,4m\) (giả sử khoảng cách các bàn như nhau).

Giả sử 4 thành phố A, B, C, D với khoảng cách (đơn vị: km) giữa các thành phố được cho bởi bảng sau:

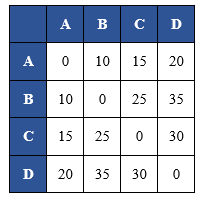
Hãy tính quãng đường ngắn nhất để đi qua tất cả các thành phố đúng một lần rồi quay lại thành phố xuất phát?

Hình dưới đây là mương dẫn nước thủy lợi tại một địa phương phục vụ tưới tiêu cho ruộng đồng. Phần không gian trong mương để nước chảy có mặt cắt ngang là hình chữ nhật \(ABCD\). Với điều kiện lưu lượng nước qua mương cho phép thì diện tích mặt cắt \(ABCD\) là \(0\,,48\,{{m}^{2}}\). Để đảm bảo yêu cầu kỹ thuật tốt nhất cho mương, người ta cần thiết kế sao cho tổng độ dài \(T=AB+\,BC+CD\) là ngắn nhất. Khi đó chiều rộng đáy mương bằng bao nhiêu (biết chiều rộng phải dưới 1m, làm tròn kết quả đến hàng phần trăm)?