Trong lớp học, màn hình tivi hình chữ nhật có chiều cao 1m được đặt ở độ cao \(1,2m\) so với tầm mắt của học sinh (tính từ đầu mép dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí ngồi sao cho góc nhìn lớn nhất (\(\widehat{BOC}\) là góc nhìn). 

Nếu xét học sinh Nam ngồi nhìn thẳng màn hình thì học sinh Nam ngồi bàn thứ mấy nhìn được rõ nhất, biết vị trí ngồi bàn đầu tiên cách tivi \(1,2m\) và mỗi bàn kế tiếp nhau cách nhau \(0,4m\) (giả sử khoảng cách các bàn như nhau).

 

Một tấm bìa cứng có kích thước \(60\text{ }\!\!~\!\!\text{ cm}\times 90\text{ }\!\!~\!\!\text{ cm}\) được gấp đôi thành một hình chữ nhật \(60\text{ }\!\!~\!\!\text{ cm}\times 45\text{ }\!\!~\!\!\text{ cm}\) như hình vẽ. Sau đó, cắt ra từ các góc của hình chữ nhật vừa gấp bốn hình vuông bằng nhau có cạnh \(x\left( \text{cm} \right)\). Tấm bìa được mở ra và sáu mép được gấp lên để tạo thành một hộp chữ nhật \(\left( \mathbf{H} \right)\) có nắp và đáy (như hình vẽ). Thể tích lớn nhất của khối \(\left( \mathbf{H} \right)\) bằng bao nhiêu lít? (làm tròn kết quả đến hàng phần mười).

Một bể cá đầy nước có dạng hình hộp chữ nhật \(ABCD.EFGH\) với \(AB=6\left( dm \right)\), \(AD=8\left( dm \right)\) và cạnh bên bằng \(10\left( dm \right)\). Một chú cá con bơi theo những đoạn thẳng từ điểm \(G\) đến chạm mặt đáy của hồ, rồi từ điểm đó bơi đến vị trí điểm \(M\) là trung điểm của \(AF\) được mô hình hóa như hình vẽ sau:

Để đường đi ngắn nhất thì chú cá bơi đến điểm dưới đáy hồ cách \(BA\) và \(BC\) những đoạn bằng \(a\) và \(b\). Khi đó tổng \(D=3a+6b\) bằng bao nhiêu?

Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất \(8000\) quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất \(30\) quả bóng trong một giờ. Chi phí thiết lập các máy này là \(200\) nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là \(192\) nghìn đồng một giờ. Số máy móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động là thấp nhất?

Nhà ông Hải có một cái cổng hình chữ nhật, lối vào cổng có dạng parabol có kích thước như hình vẽ.

Ông Hải cần trang trí bề mặt (phần gạch chéo) của cổng. Hỏi ông Hải cần bao nhiêu tiền (đơn vị: triệu đồng) để trang trí, biết giá thành trang trí là 1200000 đồng/m²?

Nhà máy \(A\) chuyên sản xuất một loại sản phẩm cho nhà máy \(B\). Hai nhà máy thỏa thuận rằng, hằng tháng \(A\) cung cấp cho \(B\) số lượng sản phẩm theo đơn đặt hàng của \(B\) (tối đa \(100\) tấn sản phẩm). Nếu số lượng đặt hàng là \(X\) tấn sản phẩm thì giá bán cho mỗi sản phẩm là \(P\left( x \right)=45-0,001{{x}^{2}}\) (triệu đồng). Chi phí để \(A\) sản xuất x tấn sản phẩm trong một tháng là \(C\left( x \right)=100+30x\) triệu đồng (gồm \(100\) triệu đồng chi phí cố định và \(30\) triệu đồng cho mỗi tấn sản phẩm). Nhà máy\(A\) bán cho \(B\) bao nhiêu tấn sản phẩm để lợi nhuận thu được là lớn nhất? (làm tròn kết quả đến hàng phần mười).

Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức \(G\left( x \right)=0,024{{x}^{2}}\left( 30-x \right)\), trong đó \(x\) là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp (x được tính bằng mg). Tìm lượng thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất.

Ông Toàn có một mảnh đất phẳng hình elip có độ dài trục lớn bằng \({16}\) m và độ dài trục nhỏ là \({10}\) m. Ông để một dải đất rộng \({8}\) m làm sân, lối đi và dải đất này nhận trục bé của elip làm trục đối xứng đồng thời ông muốn trồnghoa hai bên mảnh đất còn lại. Biết kinh phí để trồng hoa là \({100\,000}\) đồng/m\({^2}\). Hỏi ông Toàn cần bao nhiêu triệu đồng trồng hoa trên phần đất đó (kết quả được làm tròn đến hàng trăm)?

Một doanh nghiệp dự định sản xuất không quá 500 sản phẩm. Nếu doanh nghiệp sản xuất \(x\) sản phẩm \(\left( 1\le x\le 500 \right)\) thì doanh thu nhận được khi bán hết số sân phẳm đó là: \(F\left( x \right)={{x}^{3}}-1999{{x}^{2}}+1001000x+250000\) (đồng), trong khi chi phí sản xuất bình quân cho một sản phẩm là: \(G\left( x \right)=x+1000+\frac{250000}{x}\) (đồng).

Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất?

Nhằm nâng cao cơ sở vật chất cho trường, anh Hùng đang cần đặt hàng làm một chiếc bảng tương tác thông minh hình chữ nhật \(a\times b\) có chức năng cảm ứng để phục vụ cho việc dạy học, biết rằng nếu cả chiều \(b\) đều tăng thêm một nửa thì bảng sẽ có kích thước là 85 inch (quy ước \(1\text{ }inch=2,54cm\) và kích thước ấy được đo bởi đường chéo của màn hình). Tiếp đến anh Hùng muốn phủ lớp chống lóe với 7500 đồng cho mỗi mét vuông trên màn (xem như độ dày của phần phủ là không đáng kể) và 15000 đồng mỗi mét phần silicon được dán ở viền ngoài cùng của màn hình. Vậy tổng số tiền cao nhất anh Hùng có thể bỏ ra để phủ lớp chống lóe và dán silicon là bao nhiêu nghìn đồng? (làm tròn đến phần nguyên).

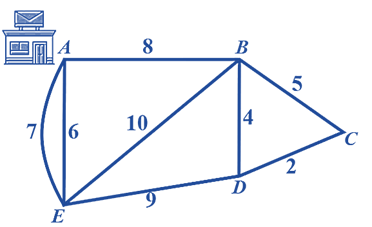
Một người đưa thư xuất phát từ bưu điện ở vị trí A, các điểm cần phát thư nằm dọc các con dường cần đi quBiết rằng người này phải đi trên mỗi con đường ít nhất một lần (để phát được thư cho tất cả các điểm cần phát nằm dọc theo con đường đó) và cuối cùng quay lại điểm xuất phát. Độ dài các con đường như hình vẽ (đơn vị độ dài). Hỏi tổng quãng đường người đưa thư có thể đi ngắn nhất có thể là bao nhiêu?

Một người nông dân có 15 000 000 đồng để làm một cái hàng rào hình chữ E dọc theo con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí vật liệu là 60 000 đồng một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng một mét. Tìm diện tích lớn nhất của đất rào thu được.

Một người đàn ông muốn chèo thuyền ở vị trí \(A\) tới điểm \(B\) về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng \(3\,\,\text{km}\) (như hình vẽ).

Anh có thể chèo thuyền của mình trực tiếp qua sông để đến \(C\) và sau đó chạy đến \(B\), hay có thể chèo trực tiếp đến \(B\), hoặc anh ta có thể chèo thuyền đến một điểm \(D\) giữa \(C\) và \(B\) và sau đó chạy đến \(B\). Biết anh ấy có thể chèo thuyền \(6\,\,\text{km/}\,\text{h}\), chạy \(8\,\,\text{km/}\,\text{h}\) và quãng đường \(BC=8\,\,\text{km}\). Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Gọi \(x\,\,\left( \text{km} \right)\) là độ dài quãng đường \(BD\). Xét tính đúng sai trong các khẳng định sau:

Một ông chủ nhà muốn làm một cái thang cứu hộ khi có nguy hiểm xảy ra. Ông ta muốn làm cái thang để nó đứng dưới đất vươn qua hàng rào tựa vào ngôi nhà. Với hàng rào cao 2,4 mét được đặt song song và cách bức tường của ngôi nhà một khoảng bằng 1,5 mét. Chiều dài ngắn nhất của cây thang bao nhiêu mét để nó đứng dưới đất vươn qua hàng rào tựa vào ngôi nhà (tham khảo hình vẽ) (làm tròn đến chữ số thập phân thứ 2)?

Một nhà máy sản xuất \(\text{ }x\) sản phẩm trong mỗi tháng. Chi phí sản xuất \(x\) sản phẩm được cho bởi hàm chi phí

\(C\left( x \right)=16\,000+500x-1,6{{x}^{2}}+0,004{{x}^{3}}\) (nghìn đồng).

Biết giá bán của của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm \(x\) và được cho bởi công thức \(p\left( x \right)=1700-7x\) (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ được tiêu thụ hết.

Một vật đang chuyển động đều với vận tốc \(v_0\) (m/s) thì bắt đầu tăng tốc với gia tốc \(a(t) = v_0t+t^2\) (m/s\(^2\)), trong đó \(t\) là khoảng thời gian được tính bằng giây kể từ thời điểm vật bắt đầu tăng tốc. Biết quãng đường vật đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng tốc là 100 m. Tính vận tốc ban đầu \(v_0\) (m/s) của vật (làm tròn đến hàng phần mười).

Giám đốc một nhà hát A đang phân vân trong việc xác định mức giá vé xem các chương trình được trình chiếu trong nhà hát. Việc này rất quan trọng nó sẽ quyết định nhà hát thu được bao nhiêu lợi nhuận từ các buổi trình chiếu. Theo kết quả kinh doanh của mình, ông ta xác định được rằng: nếu giá vé vào cửa là 20 (nghìn đồng) /người thì trung bình có 1000 người đến xem. Nhưng nếu tăng thêm 1 (nghìn đồng) /người thì sẽ mất 100 khách hàng hoặc giảm đi 1 (nghìn đồng) /người thì sẽ có thêm 100 khách hàng trong số trung bình. Biết rằng, trung bình, mỗi khách hàng còn đem lại 2 (nghìn đồng) lợi nhuận cho nhà hát trong các dịch vụ đi kèm. Hãy giúp giám đốc nhà hát này xác định xem cần tính giá vé vào cửa là bao nhiêu để thu nhập là lớn nhất.

Một sợi dây kim loại dài \(60cm\) được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh \(a\),  đoạn dây thứ hai uốn thành đường tròn bán kính \(r\) 

Ông Toàn có một mảnh đất phẳng hình elip có độ dài trục lớn bằng \({16}\) m và độ dài trục nhỏ là \({10}\) m. Ông để một dải đất rộng \({8}\) m làm sân, lối đi và dải đất này nhận trục bé của elip làm trục đối xứng đồng thời ông muốn trồnghoa hai bên mảnh đất còn lại. Biết kinh phí để trồng hoa là \({100\,000}\) đồng/m\({^2}\). Hỏi ông Toàn cần bao nhiêu triệu đồng trồng hoa trên phần đất đó (kết quả được làm tròn đến hàng trăm)?

Một căn nhà bỏ hoang có dạng hình lập phương cạnh bằng 5m có 3 chú nhện sinh sống. Mùa đông đến, vì đói rét nên chúng đành quyết định hợp tác với nhau giăng lưới để bắt mồi. Ba chú nhện tính toán sẽ giăng một mảnh lưới hình tam giác theo cách sau: Mỗi chú nhện sẽ đứng ở mép tường bất kỳ ( có thể mép giữa 2 bức tường,giữa tường với trần nhà, hoặc giữa tường với với nền), rồi phóng những sợi tơ làm khung đến vị trí của 2 con nhện còn lại rồi sau đó mới phóng tơ dính đan phần lưới bên trong. Chúng quy định không có bất kỳ 2 con nhện nào nằm cùng trên một mặt tường, nền hoặc trần nhà. Chu vi nhỏ nhất của mảnh lưới ấy (các sợi tơ khung căn và không chùm) là \(\frac{m\sqrt{n}}{p}\) (với \(m,n,p\in {{\mathbb{N}}^{*}}\)) và \(\frac{m}{p}\) là phân số tối giản. Tính giá trị của biểu thức \(m+n+p\) ?

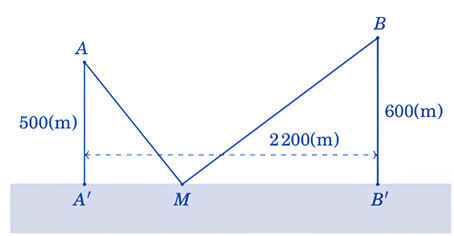
Có hai xã \(A,\,B\) cùng ở một bên bờ sông. Khoảng cách từ hai xã đó đến bờ sông lần lượt là \(A{A}'=500m\), \(B{B}'=600m\). Người ta đo được \({A}'{B}'=2200m\) như hình vẽ dưới đây. Các kỹ sư muốn xây dựng một trạm cung cấp nước sạch nằm bên bờ sông cho người dân của hai xã sử dụng. Để tiết kiệm chi phí, các kỹ sư phải chọn một vị trí \(M\) của trạm cung cấp nước sạch đó trên đoạn \({A}'{B}'\) sao cho tổng khoảng cách từ hai xã đến vị trí \(M\) là nhỏ nhất. Giá trị nhỏ nhất của tổng khoảng cách đó bằng bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị).