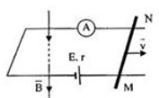
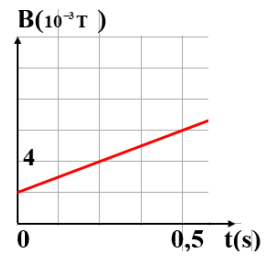
Một khung dây hình chữ nhật kín gồm N = 10 vòng dây, diện tích mỗi vòng S = 20 cm2 đặt trong một từ trường đều có véc tơ cảm ứng từ vecto B hợp với pháp tuyến vecto n của mặt phẳng khung dây góc α = 60o, độ lớn cảm ứng từ B = 0,04 T, điện trở khung dây R = 0,2 Ω. Tính cường độ dòng điện xuất hiện trong khung dây cảm ứng từ tăng đều từ 0 đến 0,5B, xuất hiện trong khung dây nếu trong thời gian Δt = 0,01 giây.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiBiến thiên từ thông: \(\Delta \Phi {\rm{ }} = {\rm{ }}{\Phi _2}\;--{\rm{ }}{\Phi _1}\; = {\rm{ }}NS({B_2}\;-{\rm{ }}{B_1}).cos\alpha = {10.20.10^{ - 4}}.(0,5.0,04 - 0)cos{60^0} = {2.10^{ - 4}}\left( {Wb} \right)\)
Suất điện động cảm ứng: \({e_c} = \left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = \left| {\frac{{{{2.10}^{ - 4}}}}{{0,01}}} \right| = 0,02V\)
Cường độ dòng điện xuất hiện trong khung: \(i = \frac{{{e_c}}}{R} = \frac{{0,02}}{{0,2}} = 0,1A\)



.png)
.png)











