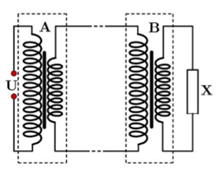
Điện năng được truyền tải từ máy hạ áp A đến máy hạ áp B bằng đường dây tải điện một pha như sơ đồ hình bên. Cuộn sơ cấp của A được nối với điện áp xoay chiều có giá trị hiệu dụng U không đổi, cuộn thứ cấp của B được nối với tải tiêu thụ X. Gọi tỉ số giữa số vòng dây của cuộn sơ cấp và số vòng dây của cuộn thứ cấp của A là k1, tỉ số giữa số vòng dây của cuộn sơ cấp và số vòng dây của cuộn thứ cấp của B là k2. Ở tải tiêu thụ, điện áp hiệu dụng như nhau, công suất tiêu thụ điện như nhau trong hai trường hợp: k1 = 33 và k2= 62 hoặc k1 = 14 và k2 = 160. Coi các máy hạ áp là lí tưởng, hệ số công suất của các mạch điện luôn bằng 1. Khi k1 = 14 và k2 = 160 thì tỉ số công suất hao phí trên đường dây truyền tải và công suất ở tải tiêu thụ là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi:
+ Hiệu điện thế cuộn sơ cấp và thứ cấp của máy hạ áp A là: \(U_1;U_2\)
+ Hiệu điện thế cuộn sơ cấp và thứ cấp của máy hạ áp B là: \(U_3;U_4\)
+ Cường độ dòng điện trên đường dây truyền tải vè trên mạch tiêu thụ lần lượt là \(I_3;I_4\)
Theo đề bài, ta có: \(\begin{array}{l} {U_1} = h/s\\ {U_4} = h/s\\ {I_4} = h/s \end{array}\)
Mà:
Ta có: \(\left\{ \begin{array}{l}
{k_1} = \frac{{{U_1}}}{{{U_2}}}\\
{k_2} = \frac{{{U_3}}}{{{U_4}}}
\end{array} \right. \to \left\{ \begin{array}{l}
{U_2} = \frac{{{U_1}}}{{{k_1}}}\\
{k_2}{U_4} = {U_3}
\end{array} \right.\)
Lại có: \( {k_2} = \frac{{{I_4}}}{{{I_3}}} \Rightarrow {I_3} = \frac{{{I_4}}}{{{k_2}}}\)
Tỉ số công suất hao phí trên dây truyền tải và công suất ở tải tiêu thụ là:
\(\begin{array}{l} \frac{{{P_R}}}{{{P_X}}}\\ \frac{{{P_R}}}{{{P_X}}} = \frac{{{U_R}{I_R}}}{{{U_X}{I_X}}} = \frac{{\left( {{U_2} - {U_3}} \right){I_3}}}{{{U_4}{I_4}}} = \frac{{{U_1}}}{{{k_1}{k_2}{U_4}}} - 1 \end{array}\)
Xét mạch truyền tải, ta có:
\(\begin{array}{*{20}{l}} { \Leftrightarrow \frac{{{U_1}{k_2}}}{{{k_1}}} - {U_4}k_2^2 = {I_4}R = h/s \Rightarrow \frac{{{U_1}{k_{2\left( 1 \right)}}}}{{{k_{1\left( 1 \right)}}}} - {U_4}k_{2\left( 1 \right)}^2 = \frac{{{U_1}{k_{2\left( 2 \right)}}}}{{{k_{1\left( 2 \right)}}}} - {U_4}k_{2\left( 2 \right)}^2 = {I_4}R}\\ { \Rightarrow {U_1}\frac{{62}}{{33}} - {U_4}{{.62}^2} = {U_1}\frac{{160}}{{14}} - {U_4}{{.160}^2} \Rightarrow \frac{{{U_1}}}{{{U_4}}} = \frac{{21756}}{{\frac{{2206}}{{231}}}} = 2278,17} \end{array}\)
Thay \(\left\{ \begin{array}{l} {k_1} = 14\\ {k_2} = 160\\ \frac{{{U_1}}}{{{U_4}}} = \frac{{52640}}{{23}} \end{array} \right.\)
vào (1) ta suy ra: \( \frac{{{P_R}}}{{{P_X}}} \approx 0,017\)