Con lắc đơn trong phòng thí nghiệm có T = 2s được treo vào trần một ô tô. Cho \(g = \pi^2 m/s^2 \) . Biết ôtô lên dốc nhanh dần đều với gia tốc \(a = \sqrt3 g \). Biết dốc nghiêng một góc \(\beta = 30^0\) so với phương ngang. Hãy xác định vị trí cân bằng của con lắc và chu kì dao động nhỏ của nó ?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
+ Chu kì dao động của con lắc đơn khi ở trong phòng thí nghiệm: \( T = 2\pi \sqrt {\frac{l}{g}} \)
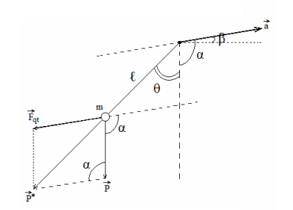
+ Oto lên nhanh dần trên dốc nghiêng (\( \vec a\) xiên lên) \( \to \overrightarrow {{F_{qt}}} \) xiên xuống
Ta có:
\(\begin{array}{*{20}{l}} {P' = \sqrt {{P^2} + F_{qt}^2 - 2P{F_{qt}}{\rm{cos}}(90 + \beta )} }\\ { \to g' = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os}}(90 + \beta )} = \sqrt {{g^2} + {a^2} - 2g.a.c{\rm{os}}(90 + {{30}^0})} = 2,394g}\\ {\frac{{T'}}{T} = \sqrt {\frac{g}{{g'}}} = \sqrt {\frac{g}{{2,394g}}} = 0,646 \to T' = 0,646.2 = 1,293{\rm{s}}} \end{array}\)
Góc θ:
\( \frac{a}{{\sin \theta }} = \frac{{g'}}{{\sin ({{90}^0} + \beta )}} \to \sin \theta = \frac{{a\sin ({{90}^0} + \beta )}}{{g'}} = \frac{{\sqrt 3 g.\sin ({{90}^0} + 30)}}{{2,394g}} = 0,627 \to \alpha = {38^0}{49^\prime }44\)



.PNG)











