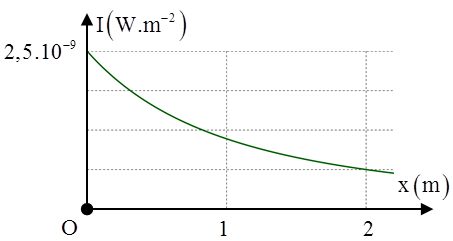
Tại một điểm trên trục Ox có một nguồn âm điểm phát âm đẳng hướng ra môi trường. Hình bên là đồ thị biểu diễn sự phụ thuộc của cường độ âm I tại những điểm trên trục Ox theo tọa độ x. Cường độ âm chuẩn là \({{I}_{0}}={{10}^{-12}}\text{ W}.{{m}^{-2}}\). M là một điểm trên trục Ox có tọa độ x = 4 m. Mức cường độ âm tại M có giá trị gần nhất với giá trị nào sau đây?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiDựa vào đồ thị, ta có
+ Cường độ âm tại O là \({{I}_{O}}=2,{{5.10}^{-9}}\text{ W/}{{\text{m}}^{2}}.\)
+ Cường độ âm tại điểm N có xN = 2 m là \({{I}_{N}}=\frac{2,{{5.10}^{-9}}}{4}=6,{{25.10}^{-10}}\text{ W/}{{\text{m}}^{2}}.\)
Ta có: \(\frac{{{I}_{O}}}{{{I}_{N}}}=\frac{R_{N}^{2}}{R_{O}^{2}}\Leftrightarrow 4=\frac{{{\left( {{R}_{O}}+{{x}_{N}} \right)}^{2}}}{R_{O}^{2}}\Leftrightarrow 2=\frac{{{R}_{O}}+2}{{{R}_{O}}}\Rightarrow {{R}_{O}}=2\text{ m}\text{.}\)
Đối với điểm M và O, ta có:
\(\frac{{{I}_{O}}}{{{I}_{M}}}=\frac{R_{M}^{2}}{R_{O}^{2}}=\frac{{{\left( {{R}_{O}}+{{x}_{M}} \right)}^{2}}}{R_{O}^{2}}=\frac{{{6}^{2}}}{{{2}^{2}}}=9\Rightarrow {{I}_{_{M}}}=\frac{{{I}_{O}}}{9}=\frac{5}{18}\text{.1}{{\text{0}}^{-9}}\text{ W/}{{\text{m}}^{2}}\text{.}\)
Mức cường độ âm taị điểm M: \({{L}_{M}}=10\log \frac{{{I}_{M}}}{{{I}_{0}}}=10\log \frac{{{5.10}^{-9}}}{{{18.10}^{-12}}}=24,4\text{ dB}\text{.}\)














