Đề thi minh họa Đánh giá tư duy Đại học Bách Khoa Hà Nội năm 2025 - Đề 1
40 câu hỏi 60 phút
Biết rằng \(F\left( x \right)=\text{ln}\left| 2x+1 \right|\) là một nguyên hàm của hàm số \(f\left( x \right)=\frac{2}{2x+1}\). Cho \(\int\limits_{0}^{4}{\frac{dx}{2x+1}}=\text{ln}S\). Khi đó giá trị của \(S\) là:
3
9
81
8
Ta có \(\int _{0}^{4}\frac{{{d}_{x}}}{2x+1}=\frac{1}{2}. \int _{0}^{4}\frac{2}{2x+1}{{d}_{x}}=\frac{1}{2}.\left( \text{ln}\left| 2. 4+1\left| -\text{ln} \right|2.0+1 \right| \right)=\text{ln}3\).
Danh sách câu hỏi:
Ta có \(\int _{0}^{4}\frac{{{d}_{x}}}{2x+1}=\frac{1}{2}. \int _{0}^{4}\frac{2}{2x+1}{{d}_{x}}=\frac{1}{2}.\left( \text{ln}\left| 2. 4+1\left| -\text{ln} \right|2.0+1 \right| \right)=\text{ln}3\).
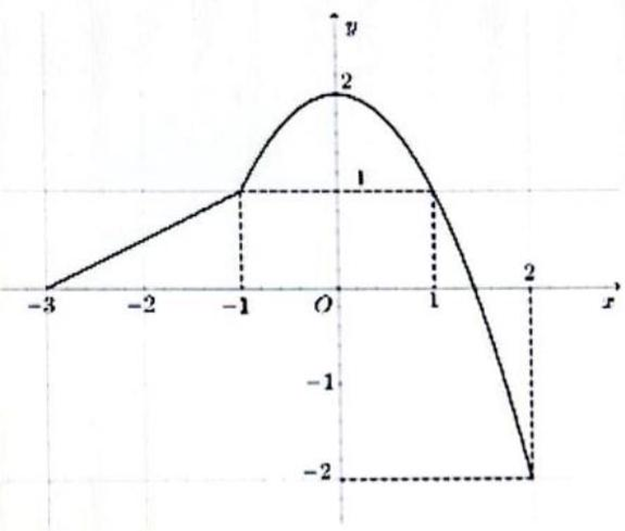
Quan sát đồ thị ta dễ dàng nhận thấy \(f\left( x \right)\) đạt giá trị lớn nhất bằng 2 khi \(x=0\) và giá trị nhỏ nhất bằng -2 khi \(x=2\).
Có 5 màu và 6 cơ do vậy tổng loại áo được sản xuất là: \(5.6=30\).
Ta có:
\(P\left( AB \right)=P\left( A \right)+P\left( B \right)-P\left( A\cup B \right)=0,075\).
\(P\left( A|B \right)=\frac{P\left( AB \right)}{P\left( B \right)}=0,25\).
Ta có: \(\left( S \right):{{(x-1)}^{2}}+{{(y+2)}^{2}}+{{(z-m)}^{2}}=m+5\).
Theo công thức tính diện tích mặt cầu ta được:
\({{S}_{xq}}=4\pi {{R}^{2}}=100\pi \Leftrightarrow {{R}^{2}}=25\Leftrightarrow m+5=25\Leftrightarrow m=20.\)
Câu 6:
Cho \(a<b\) và hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ a,b \right]\). Hãy xác định tính đúng, sai của mỗi phát biểu sau
\(\int\limits_{a}^{b}{kf\left( x \right)dx}=k\int\limits_{a}^{b}{f\left( x \right)dx}\) (k là hằng số)
\(\int\limits_{a}^{b}{f\left( x \right)dx}=\int\limits_{b}^{a}{kf\left( x \right)dx}\)
Câu 8:
Mỗi phát biểu sau đúng hay sai:
Hai đường thẳng song song thì đồng phẳng
Hai đường thẳng chéo nhau thì không có điểm chung
Hai đường thẳng không có điểm chung thì chéo nhau
Hai đường thẳng chéo nhau thì không đồng phẳng
Câu 16:
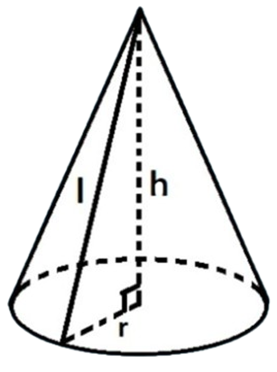
Cho một hình nón có thiết diện qua trục là tam giác đều có diện tích bằng \(2\sqrt{3}\).
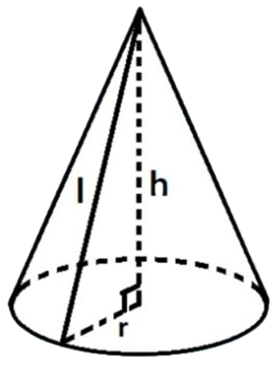
Mỗi phát biểu sau là đúng hay sai?
Bán kính đáy của hình nón đã cho bẳng \(\sqrt{2}\)
Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng \(\frac{\pi \sqrt{6}}{3}\)
Câu 20:
Cho phương trình \(\text{lo}{{\text{g}}_{2}}\sqrt{\left| x \right|}-4\sqrt{\text{lo}{{\text{g}}_{4}}\left| x \right|}-5=0\).
Các khẳng định sau là đúng hay sai?
Điều kiện xác định của phương trình là \(-1\le x\le 1\)
Đặt \(\sqrt{\frac{1}{2}\text{lo}{{\text{g}}_{2}}\left| x \right|}=t,t\ge 0\) thì phương trinh trở thành \(2{{t}^{2}}-t-5=0\)
Phương trình có 2 nghiệm phân biệt
Câu 21:
Phương trình \({{25}^{x}}+{{15}^{x}}={{6.9}^{x}}\) có một nghiệm duy nhất được viết dưới dạng \(\frac{a}{\text{lo}{{\text{g}}_{b}}c-\text{lo}{{\text{g}}_{b}}d}\) với \(a\) là số nguyên dương và \(b,c,d\) là các số nguyên tố.
Mỗi phát biểu sau là đúng hay sai?
a là số nguyên tố
b là số chẵn
Tổng \(S={{a}^{2}}+b+c+d=10\)
Câu 26:
Bạn Sơn tìm nghiệm \(x\in \left[ 0;2\pi \right)\) của ba phương trình sau đây:
• Phương trình (1): \(\text{cos}x=1\);
• Phương trình (2): \(\text{sin}x=\frac{1}{2}\);
• Phương trình (3): \(\text{sin}x+\text{cos}x=\frac{3}{2}\).
Mỗi phát biểu sau đây của bạn Sơn về các phương trình trên là đúng hay sai?
Phương trình (1) có nghiệm duy nhất trên \(\left[ 0;2\pi \right)\)
Phương trình (2) có 2 nghiệm phân biệt trên \([0;2\pi \))
Phương trình (3) có 3 nghiệm phân biệt trên \(\left[ 0;2\pi \right)\)
Câu 28:
Xét hình đa diện \(\left( H \right)\) có tất cả các mặt là ngũ giác.
Mỗi phát biểu sau là đúng hay sai?
Số cạnh của \(\left( H \right)\) là một số chia hết cho 5
Số mặt của \(\left( H \right)\) là một số chẵn
Số mặt của \(\left( H \right)\) là một số chẵn
Câu 29:
Cho dãy số \(\left( {{u}_{n}} \right)\) xác định bởi \({{u}_{1}}=1,{{u}_{n}}=3\left( {{u}_{n-1}}+2 \right)\) với mọi \(n\ge 2\). Đặt \({{v}_{n}}={{u}_{n}}+3\) với mọi \(n\in {{\mathbb{N}}^{\text{*}}}\). Mỗi phát biểu sau về các dãy số \(\left( {{u}_{n}} \right)\) và \(\left( {{v}_{n}} \right)\) là đúng hay sai?
\(\left( {{v}_{n}} \right)\) là một cấp số nhân với công sai \(q=3\)
Số hạng tổng quát của dãy số \(\left( {{v}_{n}} \right)\) là \({{v}_{n}}={{3}^{n}}\)
Số hạng tông quát: \({{u}_{n}}={{4.3}^{n-1}}-3\) với mọi \(n\in {{\mathbb{N}}^{\text{*}}}\)
Câu 32:
Cho hàm số \(f\left( x \right)\) xác định và có đạo hàm đến cấp hai trên \(\mathbb{R}\), thỏa mãn phương trình
\({{\left( {f}'\left( x \right) \right)}^{2}}+f\left( x \right)\cdot {f}''\left( x \right)=\) \(20{{x}^{4}}+12{{x}^{2}}+9,\forall x\in \mathbb{R}\) và \(f\left( 0 \right)=0\).
Biết rằng vế trái của phương trình có thể biểu diễn dưới dạng đạo hàm của một hàm số.
Mỗi phát biểu sau là đúng hay sai?
\(f\left( x \right)\cdot {f}'\left( x \right)=4{{x}^{5}}+4{{x}^{3}}+9x\)
\({{f}^{2}}\left( x \right)=\frac{2}{3}{{x}^{6}}+{{x}^{4}}+\frac{9}{2}{{x}^{2}}\)
Câu 33:
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên các khoảng \(\left( -\infty ;1 \right)\) và \(\left( 1;+\infty \right)\), có bảng biến thiên như sau.
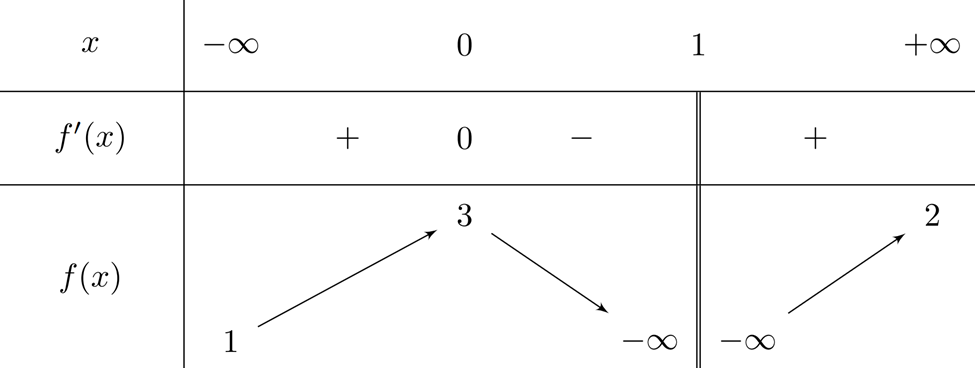
Xét tính đúng, sai của các câu sau:
Số tiệm cận đứng của đồ thị hàm số \(y=h\left( x \right)=\frac{5}{{{f}^{2}}\left( x \right)-4f\left( x \right)+3}\) là 2
Số tiệm cận ngang của đồ thị hàm số \(y=h\left( x \right)\) là 1
Tổng số tiệm cận đứng và tiẹ̀m cận ngang cưa đồ thị hàm số \(y=h\left( x \right)\) là 3
Câu 35:
Cho dãy số \(\left( {{u}_{n}} \right)\) xác định bởi \(\left\{ \begin{array}{*{35}{l}} {{u}_{1}}=5; \\ {{u}_{n+1}}=3{{u}_{n}}-7,\forall n\ge 1 \\\end{array} \right.\).
Các phát biểu sau là đúng hay sai?
Dãy số \(\left( {{u}_{n}} \right)\) là một cấp số cộng
Dãy số \(\left( {{u}_{n}} \right)\) là một cấp số nhân
Đặt \({{v}_{n}}={{u}_{n}}+\alpha \). Dãy số (\({{v}_{n}}\)) là một cấp số nhân khi và chỉ khi \(\alpha =\frac{7}{3}\)
Công thức số hạng tổng quát \({{u}_{n}}=\frac{{{3}^{n}}+7}{2}\)