Câu hỏi:
Điền số nguyên dương thích hợp vào chỗ trống.
Cho tứ diện \(ABCD\). Lấy hai điểm \(M,N\) lần lượt là trọng tâm của các tam giác \(ABC\) và \(ABD\). Cho các khẳng định sau:
1) \(MN//\left( BCD \right)\).
2) \(MN//\left( ACD \right)\).
3) \(MN//\left( ABD \right)\).
Trong các khẳng định trên, có (……) khẳng định đúng.
Đáp án đúng: 2
Dễ thấy \(\text{MN}//\left( \text{BCD} \right)\) và \(\text{MN}//\left( \text{ACD} \right)\) do \(\text{MN}//\text{CD}\).
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi minh họa đánh giá tư duy TSA 2025 là bài kiểm tra mô phỏng bài thi chính thức, giúp thí sinh rèn luyện khả năng tư duy logic, phân tích và giải quyết vấn đề. Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, bám sát cấu trúc đề thi chuẩn, phù hợp với các thí sinh dự kiến tham gia kỳ thi đánh giá tư duy năm 2025. Đây là tài liệu hữu ích giúp thí sinh làm quen với dạng bài thi, nâng cao kỹ năng suy luận và chuẩn bị tốt nhất cho kỳ thi chính thức.
Câu hỏi liên quan
Ta có: \({{\log }_{a}}b+6{{\log }_{b}}a=5\).
Áp dụng công thức đổi cơ số: \({{\log }_{b}}a=\frac{1}{{{\log }_{a}}b}\).
Phương trình trở thành:
\({{\log }_{a}}b+\frac{6}{{{\log }_{a}}b}=5\).
Đặt \(x={{\log }_{a}}b\), ta được:
\(x+\frac{6}{x}=5\Leftrightarrow {{x}^{2}}-5x+6=0\Leftrightarrow x=2\) hoặc \(x=3\).
Trường hợp 1: \(x=2\Rightarrow {{\log }_{a}}b=2\Rightarrow b={{a}^{2}}\).
Điều kiện: \(2\le a\le 2020\), và \(b={{a}^{2}}\le 2020\Rightarrow a\le \sqrt{2020}=44\).
\(\Rightarrow a\in \{2,3,\ldots ,44\}\) có 43 giá trị \(\Rightarrow \) có 43 cặp \((a,b)\) thỏa mãn.
Trường hợp 2: \(x=3\Rightarrow {{\log }_{a}}b=3\Rightarrow b={{a}^{3}}\).
Điều kiện: \(b={{a}^{3}}\le 2020\Rightarrow a\le \sqrt[3]{2020}=12\).
\(\Rightarrow a\in \{2,3,\ldots ,12\}\) có 11 giá trị \(\Rightarrow \) có 11 cặp \((a,b)\) thỏa mãn.
Vậy tổng số cặp \((a,b)\) thỏa mãn là: \(43+11=54\).
Cho hàm số \(f\left( x \right)\) xác định và có đạo hàm đến cấp hai trên \(\mathbb{R}\), thỏa mãn phương trình
\({{\left( {f}'\left( x \right) \right)}^{2}}+f\left( x \right)\cdot {f}''\left( x \right)=\) \(20{{x}^{4}}+12{{x}^{2}}+9,\forall x\in \mathbb{R}\) và \(f\left( 0 \right)=0\).
Biết rằng vế trái của phương trình có thể biểu diễn dưới dạng đạo hàm của một hàm số.
Mỗi phát biểu sau là đúng hay sai?
\(f\left( x \right)\cdot {f}'\left( x \right)=4{{x}^{5}}+4{{x}^{3}}+9x\)
\({{f}^{2}}\left( x \right)=\frac{2}{3}{{x}^{6}}+{{x}^{4}}+\frac{9}{2}{{x}^{2}}\)
Ta có phương trình:
\({{\left( {f}'(x) \right)}^{2}}+f(x). {f}''(x)=20{{x}^{4}}+12{{x}^{2}}+9\).
Nhận xét:
\(\frac{d}{dx}[f(x). {f}'(x)]={{\left( {f}'(x) \right)}^{2}}+f(x). {f}''(x)\).
\(\Rightarrow \frac{d}{dx}[f(x). {f}'(x)]=20{{x}^{4}}+12{{x}^{2}}+9\).
Lấy nguyên hàm hai vế:
\(f(x). {f}'(x)=\int{(20{{x}^{4}}+12{{x}^{2}}+9)}dx=4{{x}^{5}}+4{{x}^{3}}+9x+C\).
Biết \(f(0)=0\Rightarrow f(0). {f}'(0)=0\Rightarrow C=0\).
\(\Rightarrow f(x). {f}'(x)=4{{x}^{5}}+4{{x}^{3}}+9x\).
\(\Rightarrow \) Phát biểu a) đúng.
Tiếp tục: Ta có \({{f}^{2}}(x)\) có đạo hàm là:
\(\frac{d}{dx}[{{f}^{2}}(x)]=2f(x){f}'(x)=2(4{{x}^{5}}+4{{x}^{3}}+9x)=8{{x}^{5}}+8{{x}^{3}}+18x\).
Lấy nguyên hàm:
\({{f}^{2}}(x)=\int{(8{{x}^{5}}+8{{x}^{3}}+18x)}dx=\frac{8}{6}{{x}^{6}}+\frac{8}{4}{{x}^{4}}+9{{x}^{2}}+C\).
\(\Rightarrow {{f}^{2}}(x)=\frac{4}{3}{{x}^{6}}+2{{x}^{4}}+9{{x}^{2}}+C\).
Biết \(f(0)=0\Rightarrow {{f}^{2}}(0)=0\Rightarrow C=0\).
\(\Rightarrow {{f}^{2}}(x)=\frac{4}{3}{{x}^{6}}+2{{x}^{4}}+9{{x}^{2}}\).
Phát biểu b) nói \({{f}^{2}}(x)=\frac{2}{3}{{x}^{6}}+{{x}^{4}}+\frac{9}{2}{{x}^{2}}\) là sai.
Kết luận:
- Phát biểu a) đúng.
- Phát biểu b) sai.
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên các khoảng \(\left( -\infty ;1 \right)\) và \(\left( 1;+\infty \right)\), có bảng biến thiên như sau.
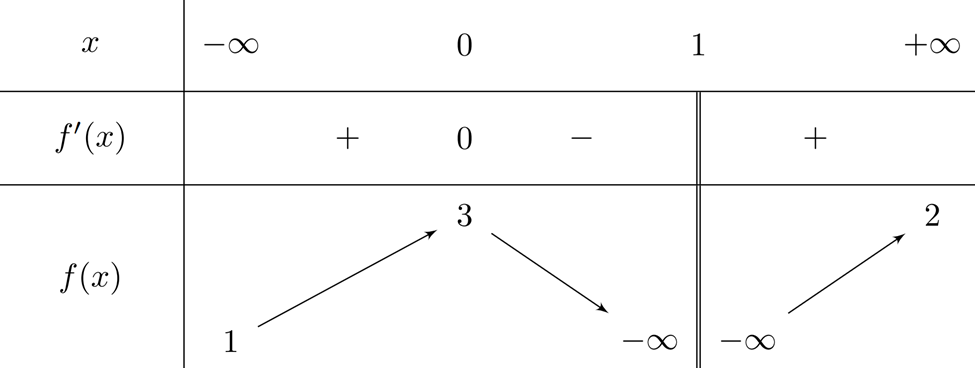
Xét tính đúng, sai của các câu sau:
Số tiệm cận đứng của đồ thị hàm số \(y=h\left( x \right)=\frac{5}{{{f}^{2}}\left( x \right)-4f\left( x \right)+3}\) là 2
Số tiệm cận ngang của đồ thị hàm số \(y=h\left( x \right)\) là 1
Tổng số tiệm cận đứng và tiẹ̀m cận ngang cưa đồ thị hàm số \(y=h\left( x \right)\) là 3
Xét hàm số \(h(x)=\frac{5}{{{f}^{2}}(x)-4f(x)+3}\).
Mẫu số bằng 0 khi:
\({{f}^{2}}(x)-4f(x)+3=0\Leftrightarrow (f(x)-1)(f(x)-3)=0\).
\(\Rightarrow \) \(f(x)=1\) hoặc \(f(x)=3\).
v Xét số nghiệm của \(f(x)=1\):
- Trên khoảng \((-\infty ,0)\), \(f(x)\) tăng từ 3 đến cực đại tại \(x=0\).
- Trên khoảng \((0,1)\), \(f(x)\) giảm đến \(+\infty \).
\(\Rightarrow \) Có 2 điểm cắt với \(f(x)=1\) trên khoảng \((-\infty ,1)\).
- Trên khoảng \((1,+\infty )\), \(f(x)\) tăng từ \(-\infty \) đến 2.
\(\Rightarrow \) Cắt thêm 1 lần nữa với \(f(x)=1\).
\(\Rightarrow \) Tổng cộng \(f(x)=1\) có 3 nghiệm phân biệt.
v Xét \(f(x)=3\):
- Khi \(x\to -\infty \), \(f(x)\to 3\) từ dưới lên, nên chạm \(f(x)=3\) đúng 1 lần
\(\Rightarrow \) \(f(x)=3\) có 1 nghiệm.
\(\Rightarrow \) Tổng số nghiệm của phương trình mẫu số \(=0\) là:
\(3+1=4\) tiệm cận đứng.
v Tiệm cận ngang:
Ta có:
\(\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=2\Rightarrow h(x)=\frac{5}{{{f}^{2}}(x)-4f(x)+3}\to \frac{5}{4-8+3}=\frac{5}{-1}=-5\).\(\underset{x\to -\infty }{\mathop{\lim }}\,f(x)=3\Rightarrow h(x)\to \frac{5}{9-12+3}=\frac{5}{0}\) (không tồn tại).
\(\Rightarrow \) Hàm số có 1 tiệm cận ngang tại \(y=-5\).
Kết luận:
- Số tiệm cận đứng là 4 \(\Rightarrow \) Phát biểu "2 tiệm cận đứng" là Sai.
- Số tiệm cận ngang là 1 \(\Rightarrow \) Phát biểu "1 tiệm cận ngang" là Đúng.
- Tổng cộng: \(4+1=5\) \(\Rightarrow \) Phát biểu "tổng là 3" là Sai.
Vì \(M\) thuộc mặt phẳng \((Oxy)\), nên tọa độ của \(M\) có dạng \(M(x;y;0)\).
Ta có:
\(A{{M}^{2}}={{(x-1)}^{2}}+{{(y-3)}^{2}}+{{(0-4)}^{2}}={{(x-1)}^{2}}+{{(y-3)}^{2}}+16\).
\(B{{M}^{2}}={{(x+1)}^{2}}+{{(y-1)}^{2}}+{{(0-2)}^{2}}={{(x+1)}^{2}}+{{(y-1)}^{2}}+4\).
\(C{{M}^{2}}={{(x-3)}^{2}}+{{(y-2)}^{2}}+{{(0+12)}^{2}}={{(x-3)}^{2}}+{{(y-2)}^{2}}+144\).
Theo đề bài, ta có \(A{{M}^{2}}+B{{M}^{2}}+C{{M}^{2}}=174\).
Thay các biểu thức đã tính ở trên vào, ta được:
\(\begin{align} & {{(x-1)}^{2}}+{{(y-3)}^{2}}+16+{{(x+1)}^{2}}+{{(y-1)}^{2}}+4+{{(x-3)}^{2}}+{{(y-2)}^{2}}+144 \\ & =174. \\ \end{align}\)
Khai triển và rút gọn phương trình trên, ta được:
\( {{x}^{2}}-2x+1+{{y}^{2}}-6y+9+16+{{x}^{2}}+2x+1+{{y}^{2}}-2y+1+4 +{{x}^{2}}-6x+9+{{y}^{2}}-4y+4+144 =174\)
\(3{{x}^{2}}-6x+3{{y}^{2}}-12y+188=174\)
\(3{{x}^{2}}-6x+3{{y}^{2}}-12y+14=0\)
\({{x}^{2}}-2x+{{y}^{2}}-4y+\frac{14}{3}=0\).
Để tìm tọa độ của \(M\), ta hoàn thành phương trình bằng cách đưa về dạng chính tắc của đường tròn:
\(\begin{array}{*{35}{l}} ({{x}^{2}}-2x+1)+({{y}^{2}}-4y+4) & =1+4-\frac{14}{3} \\ {{(x-1)}^{2}}+{{(y-2)}^{2}} & =\frac{15}{3}-\frac{14}{3} \\ {{(x-1)}^{2}}+{{(y-2)}^{2}} & =\frac{1}{3}. \\ \end{array}\)
Phương trình \({{(x-1)}^{2}}+{{(y-2)}^{2}}=\frac{1}{3}\) là phương trình của một đường tròn tâm \(I(1;2)\) và bán kính \(R=\sqrt{\frac{1}{3}}=\frac{1}{\sqrt{3}}\).
Vậy, tập hợp các điểm \(M\) thỏa mãn điều kiện đề bài là đường tròn có tâm \(I(1;2)\) và bán kính \(R=\frac{1}{\sqrt{3}}\).
Do đó, hoành độ của điểm \(M\) là 1 và tung độ của điểm \(M\) là 2.
Vậy, hoành độ của điểm \(M\) là 1 và tung độ của điểm \(M\) là 2.
Cho dãy số \(\left( {{u}_{n}} \right)\) xác định bởi \(\left\{ \begin{array}{*{35}{l}} {{u}_{1}}=5; \\ {{u}_{n+1}}=3{{u}_{n}}-7,\forall n\ge 1 \\\end{array} \right.\).
Các phát biểu sau là đúng hay sai?
Dãy số \(\left( {{u}_{n}} \right)\) là một cấp số cộng
Dãy số \(\left( {{u}_{n}} \right)\) là một cấp số nhân
Đặt \({{v}_{n}}={{u}_{n}}+\alpha \). Dãy số (\({{v}_{n}}\)) là một cấp số nhân khi và chỉ khi \(\alpha =\frac{7}{3}\)
Công thức số hạng tổng quát \({{u}_{n}}=\frac{{{3}^{n}}+7}{2}\)
a) Sai.
Ta có:
\({{u}_{n+1}}-{{u}_{n}}=3{{u}_{n}}-7-{{u}_{n}}=2{{u}_{n}}-7\).
Vì hiệu phụ thuộc vào \({{u}_{n}}\) nên không cố định.
\(\Rightarrow \) Dãy không phải cấp số cộng \(\Rightarrow \) Sai.
b) Sai.
Ta có:
\(\frac{{{u}_{n+1}}}{{{u}_{n}}}=\frac{3{{u}_{n}}-7}{{{u}_{n}}}=3-\frac{7}{{{u}_{n}}}\).
Vì tỉ số thay đổi theo \(n\) nên không cố định.
\(\Rightarrow \) Dãy không phải cấp số nhân \(\Rightarrow \) Sai.
c) Sai.
Ta có:
\({{v}_{n+1}}={{u}_{n+1}}+\alpha =3{{u}_{n}}-7+\alpha =3({{v}_{n}}-\alpha )-7+\alpha =3{{v}_{n}}-2\alpha -7\).
Để \(({{v}_{n}})\) là cấp số nhân với công bội \(q=3\), ta cần:
\({{v}_{n+1}}=3{{v}_{n}}\Rightarrow 3{{v}_{n}}-2\alpha -7=3{{v}_{n}}\Rightarrow -2\alpha -7=0\Rightarrow \alpha =-\frac{7}{2}\).
Đề cho \(\alpha =\frac{7}{3}\ne -\frac{7}{2}\).\(\Rightarrow \) Sai.
d) Đúng.
Giải phương trình truy hồi:
\({{u}_{n+1}}=3{{u}_{n}}-7\).
Đặt nghiệm tổng quát:
\({{u}_{n}}=A. {{3}^{n}}+B\).
Tìm nghiệm riêng: đặt \({{u}_{n}}=c\Rightarrow c=3c-7\Rightarrow c=\frac{7}{2}\).
Nghiệm tổng quát:
\({{u}_{n}}=A. {{3}^{n}}+\frac{7}{2}\).
Thay \({{u}_{1}}=5\) vào:
\(5=A. 3+\frac{7}{2}\Rightarrow 3A=\frac{3}{2}\Rightarrow A=\frac{1}{2}\).
Vậy:
\({{u}_{n}}=\frac{1}{2}. {{3}^{n}}+\frac{7}{2}=\frac{{{3}^{n}}+7}{2}\).
Trùng khớp với công thức đề cho \(\Rightarrow \) Đúng.

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Địa Lí 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026
ĐĂNG KÝ GÓI THI VIP
- Truy cập hơn 100K đề thi thử và chính thức các năm
- 2M câu hỏi theo các mức độ: Nhận biết – Thông hiểu – Vận dụng
- Học nhanh với 10K Flashcard Tiếng Anh theo bộ sách và chủ đề
- Đầy đủ: Mầm non – Phổ thông (K12) – Đại học – Người đi làm
- Tải toàn bộ tài liệu trên TaiLieu.VN
- Loại bỏ quảng cáo để tăng khả năng tập trung ôn luyện
- Tặng 15 ngày khi đăng ký gói 3 tháng, 30 ngày với gói 6 tháng và 60 ngày với gói 12 tháng.