Câu hỏi:
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên các khoảng \(\left( -\infty ;1 \right)\) và \(\left( 1;+\infty \right)\), có bảng biến thiên như sau.
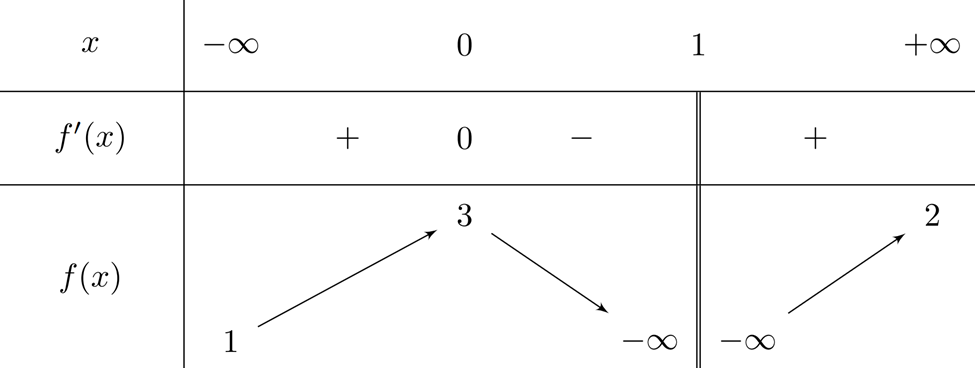
Xét tính đúng, sai của các câu sau:
Đáp án đúng: Sai, Đúng, Sai
Xét hàm số \(h(x)=\frac{5}{{{f}^{2}}(x)-4f(x)+3}\).
Mẫu số bằng 0 khi:
\({{f}^{2}}(x)-4f(x)+3=0\Leftrightarrow (f(x)-1)(f(x)-3)=0\).
\(\Rightarrow \) \(f(x)=1\) hoặc \(f(x)=3\).
v Xét số nghiệm của \(f(x)=1\):
- Trên khoảng \((-\infty ,0)\), \(f(x)\) tăng từ 3 đến cực đại tại \(x=0\).
- Trên khoảng \((0,1)\), \(f(x)\) giảm đến \(+\infty \).
\(\Rightarrow \) Có 2 điểm cắt với \(f(x)=1\) trên khoảng \((-\infty ,1)\).
- Trên khoảng \((1,+\infty )\), \(f(x)\) tăng từ \(-\infty \) đến 2.
\(\Rightarrow \) Cắt thêm 1 lần nữa với \(f(x)=1\).
\(\Rightarrow \) Tổng cộng \(f(x)=1\) có 3 nghiệm phân biệt.
v Xét \(f(x)=3\):
- Khi \(x\to -\infty \), \(f(x)\to 3\) từ dưới lên, nên chạm \(f(x)=3\) đúng 1 lần
\(\Rightarrow \) \(f(x)=3\) có 1 nghiệm.
\(\Rightarrow \) Tổng số nghiệm của phương trình mẫu số \(=0\) là:
\(3+1=4\) tiệm cận đứng.
v Tiệm cận ngang:
Ta có:
\(\underset{x\to +\infty }{\mathop{\lim }}\,f(x)=2\Rightarrow h(x)=\frac{5}{{{f}^{2}}(x)-4f(x)+3}\to \frac{5}{4-8+3}=\frac{5}{-1}=-5\).\(\underset{x\to -\infty }{\mathop{\lim }}\,f(x)=3\Rightarrow h(x)\to \frac{5}{9-12+3}=\frac{5}{0}\) (không tồn tại).
\(\Rightarrow \) Hàm số có 1 tiệm cận ngang tại \(y=-5\).
Kết luận:
- Số tiệm cận đứng là 4 \(\Rightarrow \) Phát biểu "2 tiệm cận đứng" là Sai.
- Số tiệm cận ngang là 1 \(\Rightarrow \) Phát biểu "1 tiệm cận ngang" là Đúng.
- Tổng cộng: \(4+1=5\) \(\Rightarrow \) Phát biểu "tổng là 3" là Sai.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi minh họa đánh giá tư duy TSA 2025 là bài kiểm tra mô phỏng bài thi chính thức, giúp thí sinh rèn luyện khả năng tư duy logic, phân tích và giải quyết vấn đề. Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, bám sát cấu trúc đề thi chuẩn, phù hợp với các thí sinh dự kiến tham gia kỳ thi đánh giá tư duy năm 2025. Đây là tài liệu hữu ích giúp thí sinh làm quen với dạng bài thi, nâng cao kỹ năng suy luận và chuẩn bị tốt nhất cho kỳ thi chính thức.
Câu hỏi liên quan

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – I-Learn Smart World – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Tiếng Anh 12 – Global Success – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Kết Nối Tri Thức – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Hóa Học 12 – Chân Trời Sáng Tạo – Năm Học 2025-2026

Trọn Bộ Giáo Án Word & PowerPoint Công Nghệ 12 – Kết Nối Tri Thức – Năm Học 2025-2026