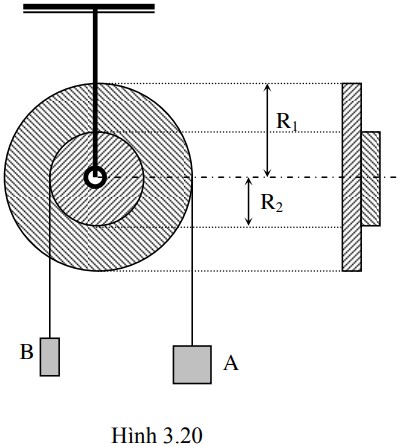
Một đĩa tròn mỏng đồng chất, khối lượng phân bố đều, bán kính R, bị khoét một lỗ hình tròn, bán kính r = R/2. Tâm O’ của lỗ thủng cách tâm O của đĩa một khoảng R/2. Khối lượng của phần còn lại là m. Mômen quán tính của phần còn lại đối với trục quay đi qua O và O’là:
Đáp án đúng: C
Gọi \(\rho\) là mật độ khối lượng trên đơn vị diện tích của đĩa. Khối lượng của đĩa ban đầu (khi chưa khoét lỗ) là: \(M = \rho \pi R^2\) Khối lượng của phần bị khoét là: \(m' = \rho \pi r^2 = \rho \pi (R/2)^2 = \frac{1}{4} \rho \pi R^2 = \frac{1}{4}M\) Vậy, khối lượng của phần còn lại là: \(m = M - m' = M - \frac{1}{4}M = \frac{3}{4}M \Rightarrow M = \frac{4}{3}m\) Mômen quán tính của đĩa ban đầu đối với trục quay đi qua O là: \(I = \frac{1}{2}MR^2 = \frac{1}{2}.\frac{4}{3}m.R^2 = \frac{2}{3}mR^2\) Mômen quán tính của phần bị khoét đối với trục quay đi qua O' là: \(I' = \frac{1}{2}m'r^2 = \frac{1}{2}.\frac{1}{4}M.(R/2)^2 = \frac{1}{32}MR^2 = \frac{1}{32}.\frac{4}{3}mR^2 = \frac{1}{24}mR^2\) Áp dụng định lý Steiner, mômen quán tính của phần bị khoét đối với trục quay đi qua O là: \(I_O' = I' + m'(OO')^2 = \frac{1}{24}mR^2 + \frac{1}{4}M.(R/2)^2 = \frac{1}{24}mR^2 + \frac{1}{4}.\frac{4}{3}m.\frac{R^2}{4} = \frac{1}{24}mR^2 + \frac{1}{12}mR^2 = \frac{1}{8}mR^2\) Mômen quán tính của phần còn lại đối với trục quay đi qua O là: \(I_{cl} = I - I_O' = \frac{2}{3}mR^2 - \frac{1}{8}mR^2 = \frac{16 - 3}{24}mR^2 = \frac{13}{24}mR^2\)
500+ câu hỏi ôn tập trắc nghiệm môn Vật lý đại cương sẽ là đề cương ôn thi hữu ích dành cho các bạn sinh viên Đại học - Cao đẳng ôn thi môn đại cương dễ dàng hơn. Mời các bạn cùng tham khảo!
Câu hỏi liên quan
Áp dụng định luật II Newton cho vật m:
P + T = ma (1) chiếu lên phương chuyển động: P - T = ma
Áp dụng phương trình mô men lực đối với trụ: M = I.γ = I.a/R
=> T.R = I.a/R => T = (I/R2).a = (m0.R2/2R2).a = m0.a/2 (2)
Từ (1) và (2) => P = ma + m0.a/2
=> a = P/(m + m0/2) = 10/(1 + 2/2) = 5 (m/s2).
.jpg)
Gọi T là lực căng dây, a là gia tốc của vật m, và α là gia tốc góc của trụ. Áp dụng định luật II Newton cho vật m: m.g - T = m.a Áp dụng phương trình mô men lực cho trụ: T.R = I.α, với I là mô men quán tính của trụ đối với trục quay và R là bán kính của trụ. Vì dây không trượt trên trụ, ta có a = α.R Mô men quán tính của trụ đặc đồng chất là I = (1/2)m₀.R² Thay các phương trình trên vào, ta có: T.R = (1/2)m₀.R². (a/R) => T = (1/2)m₀.a Từ phương trình m.g - T = m.a, ta có T = m.g - m.a Thay T = (1/2)m₀.a vào, ta có m.g - (1/2)m₀.a = m.a => m.g = m.a + (1/2)m₀.a = a(m + (1/2)m₀) => a = m.g / (m + (1/2)m₀) = 1*10 / (1 + (1/2)*2) = 10 / 2 = 5 m/s² => T = (1/2)m₀.a = (1/2)*2*5 = 5 N
Vậy lực căng dây là 5N.
Ta có phương trình chuyển động của vô lăng:
\(I\gamma = - k\sqrt \omega \Leftrightarrow I\frac{{d\omega }}{{dt}} = - k\sqrt \omega \Leftrightarrow \int_{\omega _0}^0 {\frac{{d\omega }}{{\sqrt \omega }}} = - \frac{k}{I}\int_0^t {dt} \)
\( \Leftrightarrow 2\sqrt {\omega |_{\omega _0}^0} = - \frac{k}{I}t \Leftrightarrow t = \frac{{2I\sqrt {{\omega _0}} }}{k}\)
Vận tốc góc tức thời của vô lăng:
\(\smallint_{\omega _0}^{\omega (t)} {\frac{{d\omega }}{{\sqrt \omega }}} = - \frac{k}{I}\smallint_0^t {dt} \Leftrightarrow 2(\sqrt {\omega (t)} - \sqrt {{\omega _0}} ) = - \frac{k}{I}t \Leftrightarrow \omega (t) = {(\sqrt {{\omega _0}} - \frac{k}{{2I}}t)^2}\)
Vận tốc góc trung bình của vô lăng trong thời gian hãm là:
\({\omega _{tb}} = \frac{{\smallint_0^t {\omega (t)dt} }}{t} = \frac{{\smallint_0^{\frac{{2I\sqrt {{\omega _0}} }}{k}} {{{(\sqrt {{\omega _0}} - \frac{k}{{2I}}t)}^2}dt} }{{\frac{{2I\sqrt {{\omega _0}} }}{k}}} = \frac{{{\omega _0}}}{3}\)
Để xác định vật A đi lên hay đi xuống, ta cần so sánh momen lực tác dụng lên hệ do trọng lực của vật A và vật B gây ra. Momen lực được tính bằng công thức M = rF, trong đó r là bán kính và F là lực tác dụng.
Momen lực do vật A gây ra là MA = TAR1, với TA là lực căng dây tác dụng lên vô lăng 1. Lực căng TA gần bằng trọng lực của vật A, tức là TA ≈ mAg.
Momen lực do vật B gây ra là MB = TBR2, với TB là lực căng dây tác dụng lên vô lăng 2. Tương tự, TB ≈ mBg.
Ta có MA = mAgR1 và MB = mBgR2.
Theo đề bài, R1 = 2R2, mA = 3kg, mB = 5kg.
Vậy MA = 3g(2R2) = 6gR2 và MB = 5gR2.
Vì MA > MB, nên vật A sẽ có xu hướng kéo hệ quay theo chiều của nó, tức là vật A đi xuống.
Để tính tốc độ trung bình trên toàn bộ quãng đường, ta cần tính tổng quãng đường và tổng thời gian di chuyển.
Thời gian đi đoạn AB là: tAB = sAB / vAB = 50 km / 20 km/h = 2.5 h
Độ dài đoạn BC là: sBC = vBC * tBC = 80 km/h * 3.5 h = 280 km
Độ dài đoạn CD là: sCD = 3 * sAB = 3 * 50 km = 150 km
Thời gian đi đoạn CD là: tCD = sCD / vCD = 150 km / 30 km/h = 5 h
Tổng quãng đường là: s = sAB + sBC + sCD = 50 km + 280 km + 150 km = 480 km
Tổng thời gian (bao gồm cả thời gian nghỉ) là: t = tAB + tBC + tnghỉ + tCD = 2.5 h + 3.5 h + 50/60 h + 5 h = 2.5 h + 3.5 h + 0.833 h + 5 h = 11.833 h
Tốc độ trung bình là: vtb = s / t = 480 km / 11.833 h ≈ 40.56 km/h
Trong các đáp án đã cho, đáp án gần đúng nhất là 41.7 km/h.
