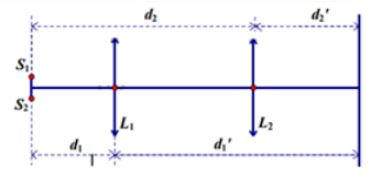
Một tấm nhôm mỏng, trên có rạch hai khe hẹp song song \({S_1}\) và \({S_2}\) và đặt cách một màn 1,2 m. Đặt giữa màn và hai khe một thấu kính hội tụ có tiêu cự \(\frac{{80}}{3}cm\), người ta tìm được hai trị trí của thấu kính cho ảnh của hai khe \({S_1}\) và \({S_2}\) rõ nét trên màn. Ở vị trí mà ảnh lớn hơn thì khoảng cách giữa hai ảnh \({S_1}'\) và \({S_2}'\) là 1,6mm. Khi bỏ thấu kính ra và chiếu sáng hai khe bằng ánh sáng đơn sắc có bước sóng \(0,6\mu m\) thì khoảng vân giao thoa trên màn là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐáp án : B
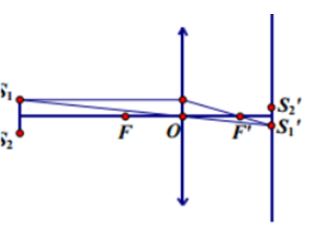
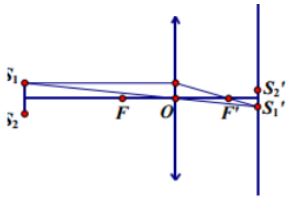
Trên hình vẽ, ta có \({L_1};{L_2}\) là 2 vị trí của thấu kính sao cho ảnh rõ nét của 2 nguồn trên màn.
Gọi \(f\) là tiêu cự của thấu kính, ta có:
+ Xét vị trí \({L_1}\): \(\frac{1}{f} = \frac{1}{{{d_1}}} + \frac{1}{{d{'_1}}}\)
+ Xét vị trí \({L_2}\): \(\frac{1}{f} = \frac{1}{{{d_2}}} + \frac{1}{{d{'_2}}}\)
\( \Rightarrow \frac{1}{{{d_1}}} + \frac{1}{{{d_1}'}} = \frac{1}{{{d_2}}} + \frac{1}{{{d_2}'}}\)
Lại có: \({d_1} + {d_1}' = {d_2} + {d_2}' = S\)
\( \Rightarrow {d_1}.{d_1}' = {d_2}{d_2}' = P\,\,\,\,\,\left( 1 \right)\)
Từ (1) ta suy ra \({d_1};{d_1}'\) là 2 nghiệm của phương trình:
\({X^2} - S{\rm{X}} + P = 0\) và \({d_2};{d_2}'\) cũng vậy.
Phương trình trên là phương trình bậc 2 có 2 nghiệm phân biệt \({X_1},{X_2}\)
Do \({d_1} \ne {d_2}\) nên \({X_1} = {d_1} = {d_2}'\) và \({X_2} = {d_2} = {d_1}'\)
Theo đề bài ta có:
\(\left\{ \begin{array}{l}{d_1} + {d_1}' = 1,2m = 120cm\\\frac{3}{{80}} = \frac{1}{{{d_1}}} + \frac{1}{{120 - {d_1}}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{d_1} = {d_2}' = 40cm\\{d_1}' = {d_2} = 80cm\end{array} \right.\)
Ta xét 1 vị trí bất kì của thấu kính
Từ hình vẽ, ta có: \({S_1}'{S_2}' = {S_1}{S_2}\frac{{d'}}{d}\)
Suy ra để có ảnh lớn hơn, ta phải có \(\frac{{d'}}{d} > 1\)
Tức là thấu kính gần \({S_1}{S_2}\) hơn
Khi đó: \(\left\{ \begin{array}{l}d = 40cm\\d' = 80cm\end{array} \right.\)
\( \Rightarrow {S_1}{S_2} = {S_1}'{S_2}'\frac{d}{{d'}} = 1,6\frac{{40}}{{80}} = 0,8mm\)
Vậy \(a = 0,8mm\)
Khi bỏ thấu kính cho giao thoa ánh sáng trên màn khi đó có khoảng vân:
\(i = \frac{{\lambda D}}{a} = \frac{{0,{{6.10}^{ - 6}}.1,2}}{{0,{{8.10}^{ - 3}}}} = {9.10^{ - 4}}m = 0,9mm\)
Đề thi thử Tốt nghiệp THPT môn Vật lí năm 2023-2024
Trường THPT Phan Đăng Lưu
Câu hỏi liên quan
-
Dao động được tạo ra bằng cách cung cấp cho hệ một năng lượng đúng bằng năng lượng nó đã mất sau mỗi chu kì gọi là dao động
-
Trong nguyên tử hiđrô, bán kính Bo là \(5,{3.10^{ - 11}}m\). Khi ở trạng thái kích thích, êlectron chuyển động trên quỹ đạo dừng L có bán kính là
-
Cho \(h = 6,{625.10^{ - 34}}J;c = {3.10^8}m/s\). Phôtôn có năng lượng \(7,{95.10^{ - 19}}J\) ứng với bức xạ thuộc vùng
-
Điện năng truyền tải đi xa thường bị hao phí chủ yếu do tỏa nhiệt trên đường dây. Gọi R là điện trở đường dây, P là công suất điện được truyền đi, U là điện áp tại nơi phát, \(co{\rm{s}}\varphi \) là hệ số công suất của mạch điện thì công suất hao phí trên đường dây là
-
Một bộ nguồn gồm n nguồn điện giống nhau. Mỗi nguồn có suất điện động \(\xi \) và điện trong r. Các nguồn này ghép song song nhau. Điện trở trong của bộ nguồn được xác định bởi biểu thức
-
Các đặc trưng sinh lí của âm bao gồm
-
Một máy biến áp có tỉ số giữa số vòng dây ở cuộn thứ cấp và sơ cấp là 10. Đặt vào hai đầu cuộn sơ cấp một điện áp xoay chiều có giá trị hiệu dụng 200V. Điện áp hiệu dụng hai đầu cuộn thứ cấp là
-
Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Mạch dao động tự do với tần số là
-
Hai con lắc lò xo nằm ngang dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của hai dao động đều nằm trên một đường thẳng qua O và vuông góc với Ox. Đồ thị (1), (2) lần lượt biểu diễn mối liên hệ giữa lực kéo về \({F_{kv}}\) và li độ x của con lắc 1 và con lắc 2. Biết tại thời điểm \({t_1}\) , hai con lắc có cùng li độ và đúng bằng biên độ của con lắc 2. Tại thời điểm \({t_2}\) sau đó, khoảng cách giữa hai vật nặng theo phương Ox là lớn nhất. Tỉ số giữa thế năng của con lắc 1 và động năng của con lắc 2 tại thời điểm \({t_2}\) là
-
Hạt nhân \(_{92}^{235}U\) có độ hụt khối \(1,91519u\). Biết \(1u{c^2} = 931,5MeV\). Năng lượng liên kết của hạt nhân này có giá trị xấp xỉ bằng
-
Ánh sáng đơn sắc là ánh sáng
-
Hai dao động điều hòa cùng phương có phương trình \({x_1} = Aco{\rm{s}}\left( {\omega t - \frac{{2\pi }}{3}} \right)cm\) và \({x_2} = Aco{\rm{s}}\left( {\omega t + \frac{\pi }{3}} \right)cm\). Độ lệch pha giữa hai dao động là
-
Một máy phát điện xoay chiều một pha có rôto là phần cảm, cần phát ra dòng điện có tần số không đổi 60 Hz để duy trì hoạt động của một thiết bị kĩ thuật. Nếu thay rôto của máy phát điện bằng một rôto khác có ít hơn hai cặp cực thì số vòng quay của rôto trong một giờ phải thay đổi đi 18000 vòng. Số cặp cực của rôto lúc đầu là
-
Tại hai điểm A, B cách nhau 14cm thuộc bề mặt chất lỏng người ta đặt hai nguồn sóng kết hợp dao động theo phương thẳng đứng với phương trình \({u_A} = {u_B} = Acos\left( {\omega t} \right)\left( {cm} \right)\). Điểm N thuộc mặt thoáng chất lỏng cách nguồn A, B lần lượt 8cm và 17cm có biên độ sóng cực đại. Giữa N và đường trung trực của AB có hai dãy cực đại khác. Xem quá trình lan truyền sóng biên độ không đổi, không tiêu hao năng lượng. Tại mặt thoáng chất lỏng, xét điểm M thuộc đường tròn tâm B bán kính AB cũng có biên độ sóng cực đại và xa điểm A nhất. Khoảng cách từ điểm B đến hình chiếu của điểm M xuống đường thẳng nối AB là
-
Sóng cơ không truyền được trong môi trường nào sau đây?
-
Một con lắc lò xo có độ cứng k dao động điều hòa theo trục Ox nằm ngang với phương trình \(x = Aco{\rm{s}}\omega {\rm{t}}\). Mốc thế năng ở vị trí cân bằng. Cơ năng của con lắc là
-
Giả sử hai hạt nhân X và Y có độ hụt khối bằng nhau và số nuclon của hạt nhân X lớn hơn số nuclôn của hạt nhân Y thì:
-
Một sóng hình sin lan truyền trong một môi trường với phương trình sóng \(u = 4co{\rm{s2}}\pi \left( {\frac{t}{{0,1}} - \frac{x}{2}} \right)\left( {cm} \right)\) (x tính bằng cm, t tính bằng giây). Tốc độ truyền sóng là
-
Quãng đường sóng truyền đi được trong một chu kì gọi là
-
Nguyên tắc hoạt động của quang điện trở dựa vào
