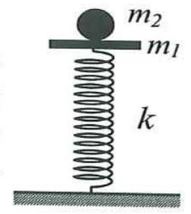
Một con lắc lò xo đặt thẳng đứng gồm lò xo nhẹ có độ cứng \(k = 100{\rm{\;N}}/{\rm{m}}\) và vật nhỏ m1 có khối lượng 200g, một đầu lò xo được gắn chặt vào sàn. Ban đầu, giữ m1 ở vị trí lò xo bị nén 7,1 cm (trong giới hạn đàn hồi của lò xo) rồi đặt vật nhỏ m2 có khối lượng 50g lên trên m1 như hình bên.
Thả nhẹ để các vật bắt đầu chuyển động theo phương thẳng đứng. Ngay khi m2 đạt độ cao cực đại thì m2 được giữ lại. Biết lò xo luôn thẳng đứng trong quá trình chuyển động. Bỏ qua lực cản của không khí. Lấy \(g = 10{\rm{\;m}}/{{\rm{s}}^2}\). Sau khi m2 được giữ lại, lực nén lớn nhất mà lò xo tác dụng lên sàn có giá trị gần nhất với giá trị nào sau đây?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn A.
Độ biến dạng của lò xo tại vị trí cân bằng
\(\Delta {l_0} = \frac{{{m_1} + {m_2}}}{k}g = \frac{{\left( {{{200.10}^{ - 3}}} \right) + \left( {{{50.10}^{ - 3}}} \right)}}{{\left( {100} \right)}}.\left( {10} \right) = 2,5\;cm\)
Giữ hai vật ở vị trí lò xo nén 7,1 cm rồi thả nhẹ ⇒ sau đó hệ hai vật dao động điều hòa quanh vị trí cân bằng với biên độ
\({A_1} = 7,1 - 2,5 = 4,6\;cm\)
Cho đến khi chúng tách rời nhau.
Giai đoạn 1: Hai vật chưa rời khỏi nhau
Tần số góc của dao động
\({\omega _1} = \sqrt {\frac{k}{{{m_1} + {m_2}}}} = \sqrt {\frac{{\left( {100} \right)}}{{\left( {{{200.10}^{ - 3}}} \right) + \left( {{{50.10}^{ - 3}}} \right)}}} = 20\frac{{rad}}{s}\)
Phương trình động lực học cho chuyển động của vật m2
\({m_2}g - N = - {m_2}\omega _1^2x\;\left( 1 \right)\)
Tại vị trí m2 rời khỏi vật m1 thì N = 0
(1) \(\Rightarrow x = - \frac{g}{{\omega _1^2}} = - \frac{{\left( {10} \right)}}{{{{\left( {20} \right)}^2}}} = - 2,5\;cm\)
\(\Rightarrow {v_{{\rm{roi}}}} = {\omega _1}{A_1}\sqrt {1 - {{\left( {\frac{x}{{{A_1}}}} \right)}^2}} \)
\(= \left( {20} \right).\left( {4,6} \right)\sqrt {1 - {{\left( {\frac{{ - 2,5}}{{4,6}}} \right)}^2}} = 77,23\frac{{cm}}{s}\)
Giai đoạn 2: Hai vật tách rời khỏi nhau
Vật m1 dao động điều hòa quanh vị trí cân bằng mới nằm trên vị trí cân bằng cũ một đoạn 0,5cm
\({\omega _2} = \sqrt {\frac{k}{{{m_1}}}} = \sqrt {\frac{{\left( {100} \right)}}{{\left( {{{200.10}^{ - 3}}} \right)}}} = 10\sqrt 5 \frac{{rad}}{s}\)
\({A_2} = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{{77,23}}{{10\sqrt 5 }}} \right)}^2}} = 3,99\;cm\)
Lực nén cực đại mà lò xo tác dụng lên sàn
\({F_{max}} = k\left( {A + \Delta l} \right)\)
\({F_{max}} = \left( {100} \right)\left[ {\left( {3,{{99.10}^{ - 2}}} \right) + \left( {{{2.10}^{ - 2}}} \right)} \right] = 5,99\;N\)
Câu hỏi liên quan
-
Tia X có cùng bản chất với tia nào sau đây?
-
Ở một nơi trên mặt đất, hai con lắc đơn có chiều dài l và l+45 (cm) cùng được kích thích để dao động điều hòa. Chọn thời điểm ban đầu là lúc dây treo của hai con lắc đều có phương thẳng đứng. Khi độ lớn góc lệ̣ch dây treo của một con lắc so với phương thẳng đứng là lớn nhất lần thứ ba thì con lắc còn lại ở vị trí có dây treo trùng với phương thẳng đứng lần thứ hai (không tính thời điểm ban đầu). Giá trị của l là:
-
Mạch chọn sóng ở một máy thu thanh là mạch dao động gồm cuộn cảm thuần có độ tự cảm \(50\mu {\rm{H}}\) và tụ điện có điện dung C thay đổi được. Lấy \({\pi ^2} = 10\). Để thu được sóng điện từ có tần số \(10{\rm{MHz}}\) thì giá trị của lúc này là:
-
Đặt một điện áp xoay chiều có tần số góc \(\omega = 100\pi {\rm{rad}}/{\rm{s}}\) vào hai đầu đoạn mạch chỉ có cuộn cảm thuần có độ tự cảm \(L = \frac{{0,2}}{\pi }{\rm{H}}\). Cảm kháng của đoạn mạch có giá trị là:
-
Âm có tần số nằm trong khoảng từ 16Hz đến 20000Hz được gọi là:
-
Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang. Mốc thế năng ở vị trí cân bằng. Khi nói về cơ năng của con lắc, phát biểu nào sau đây sai?
-
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại A và B cách nhau 9,6 cm, dao động cùng pha theo phương thẳng đứng. Ở mặt chất lỏng, P là điểm cực tiểu giao thoa cách A và B lần lượt là 15cm và 20cm, giữa P và đường trung trực của đoạn thẳng AB có hai vân giao thoa cực tiểu khác. Số điếm cực đại giao thoa trên đoạn thẳng AP là:
-
Ở một nơi trên mặt đất, con lắc đơn có chiều dài l dao động điều hòa với chu kì T. Cũng tại nơi đó, con lắc đơn có chiều dài \(\frac{l}{4}\) dao động điều hòa với chu kì là:
-
Theo thuyết lượng tử ánh sáng, mỗi lần một nguyên tử hay phân tử phát xạ ánh sáng thì chúng phát ra
-
Đặt điện áp \(u = 120\cos \left( {100\pi t - \frac{\pi }{6}} \right)\,\,(V)\) vào hai đầu đoạn mạch AB mắc nối tiếp gồm: tụ điện có điện dung C thay đổi được; cuộn dây có độ tự cảm L và điện trở r; điện trở R với R=2r như hình bên.
Khi C=C0 thì điện áp hiệu dụng giữa hai đầu đoạn mạch AN đạt cực tiểu. Khi \(C = \frac{{{C_0}}}{4}\) thì điện áp hiệu dụng giữa hai đầu đoạn mạch AM đạt cực đại và điện áp giữa hai đầu đoạn mạch MN là \({u_{{\rm{MN}}}}\). Biểu thức \({u_{{\rm{MN}}}}\) là:
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng đơn sắc, khoảng vân đo được trên màn quan sát là 0,08mm. Trên màn, khoảng cách giữa ba vân sáng liên tiếp là:
-
Giới hạn quang dẫn của PbS là \(4,14\mu {\rm{m}}\). Lấy \(h = 6,625 \cdot {10^{ - 34}}{\rm{\;J}}{\rm{.s}};c = 3 \cdot {10^8}{\rm{\;m}}/{\rm{s}}\). Năng lượng cần thiết (năng lượng kích hoạt) để giải phóng một êlectron liên kết thành êlectron dẫn của PbS là:
-
Hai dao động điều hòa cùng tần số có pha ban đầu là \({\varphi _1}\) và \({\varphi _1}\). Hai dao động này cùng pha khi
-
Một sóng cơ có chu kỳ T, lan truyền trong một môi truờng với tốc độ v. Bước sóng \(\lambda \) được xác định bằng công thức nào sau đây?
-
Theo mẫu nguyên tử Bo, nếu nguyên tử đang ở trạng thái dừng có năng lượng \({E_{\rm{m}}}\) mà hấp thụ được một phôtôn có năng lượng \({E_{\rm{n}}} - {E_{\rm{m}}}\) thì nó chuyển lên trạng thái dừng có năng lượng
-
Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số góc \(\omega \) thay đổi được vào hai đầu một đoạn mạch gồm điện trở, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Cường độ dòng điện hiệu dụng trong đoạn mạch có giá trị lớn nhất khi
-
Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số không đổi vào hai đầu đoạn mạch gồm biến trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Khi \(R = {R_1}\) thì điện áp hiệu dụng giữa hai đầu L và hai đầu C lần lượt là \({U_{\rm{L}}}\) và \({U_{\rm{C}}}\) với \({U_{\rm{C}}} = 2{U_{\rm{L}}} = U\). Khi \(R = {R_2} = \frac{{{R_1}}}{{\sqrt 3 }}\) thì điện áp hiệu dụng giữa hai đầu L là 100V. Giá trị của U là:
-
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \(R = 40{\rm{\Omega }}\) và cuộn cảm thuần có độ tự cảm \(L = \frac{1}{{2\pi }}{\rm{H}}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của điện áp \({u_{\rm{R}}}\) giữa hai đầu điện trở theo thời gian t. Biểu thức của u theo thời gian t (t tính bằng s) là:
-
Một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Độ lệch pha của cường độ dòng điện trong mạch so với điện tích của một bản tụ điện có độ lơn là
-
Một vật dẫn đang có dòng điện một chiều chạy qua. Trong khoảng thời gian \({\rm{\Delta }}t\), điện lượng dịch chuyển qua tiết diện thẳng của vật dẫn là \({\rm{\Delta }}q\). Cường độ dòng điện I trong vật dẫn được tính bằng công thức nào sau đây?
