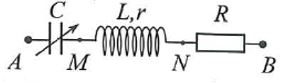
Đặt điện áp \(u = 120\cos \left( {100\pi t - \frac{\pi }{6}} \right)\,\,(V)\) vào hai đầu đoạn mạch AB mắc nối tiếp gồm: tụ điện có điện dung C thay đổi được; cuộn dây có độ tự cảm L và điện trở r; điện trở R với R=2r như hình bên.
Khi C=C0 thì điện áp hiệu dụng giữa hai đầu đoạn mạch AN đạt cực tiểu. Khi \(C = \frac{{{C_0}}}{4}\) thì điện áp hiệu dụng giữa hai đầu đoạn mạch AM đạt cực đại và điện áp giữa hai đầu đoạn mạch MN là \({u_{{\rm{MN}}}}\). Biểu thức \({u_{{\rm{MN}}}}\) là:
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn D.
Khi C = Co
\({U_{AN}} = \frac{{U\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = min\)
Ta có:
\({U_{AN}} = \frac{U}{{\sqrt {1 + \frac{{{R^2} + 2Rr}}{{{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}} }}\;\left( 1 \right)\)
\(\left( 1 \right) \Rightarrow {U_{AN}} = min\) khi
\({Z_C} = {Z_L}\)
\(\Rightarrow {Z_L} = {Z_{C0}}\;\left( 2 \right)\)
Khi \(C = \frac{{{C_0}}}{4}\) thì \({Z_C} = 4{Z_{C0}}\)
\({U_{AM}} = {U_C} = max\)
\(\Rightarrow \;{Z_C} = \frac{{{{\left( {R + r} \right)}^2} + Z_L^2}}{{{Z_L}}}\)
\(\left( {4{Z_{C0}}} \right) = \frac{{{{\left( {2r + r} \right)}^2} + {{\left( {{Z_{C0}}} \right)}^2}}}{{\left( {{Z_{C0}}} \right)}}\)
\(\Rightarrow \left\{ {\begin{array}{*{20}{c}} {r = \frac{{{Z_{C0}}}}{{\sqrt 3 }}}\\ {R = \frac{{2{Z_{C0}}}}{{\sqrt 3 }}} \end{array}} \right.\)
Phương trình điện áp hai đầu đoạn mạch MN (phức hóa)
\(\overline {{u_{MN}}} = \frac{{\overline {u\;} }}{{\overline {Z\;} }}.\overline {{Z_{MN}}} \)
\(\overline {{u_{MN}}} = \frac{{\left( {120\angle - \frac{\pi }{6}} \right)}}{{\left[ {\left( {\sqrt 3 } \right) + \left( {1 - 4} \right)i} \right]}}.\left[ {\left( {\frac{1}{{\sqrt 3 }}} \right) + \left( 1 \right)i} \right] = 40\angle \frac{\pi }{2}\)
Vậy \({u_{MN}} = 40{\rm{cos}}\left( {100\pi t + \frac{\pi }{2}} \right)V\)
Câu hỏi liên quan
-
Hai điện tích điểm gây ra tại điểm M hai điện trường có các vectơ cuờng độ điện truờng \(\overrightarrow {{E_1}} \) và \(\overrightarrow {{E_2}} \). Vectơ cường độ điện trường tổng hợp \(\vec E\) tại M được tính bằng công thức nào sau đây?
-
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \(R = 40{\rm{\Omega }}\) và cuộn cảm thuần có độ tự cảm \(L = \frac{1}{{2\pi }}{\rm{H}}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của điện áp \({u_{\rm{R}}}\) giữa hai đầu điện trở theo thời gian t. Biểu thức của u theo thời gian t (t tính bằng s) là:
-
Đặt một điện áp xoay chiều có tần số góc \(\omega = 100\pi {\rm{rad}}/{\rm{s}}\) vào hai đầu đoạn mạch chỉ có cuộn cảm thuần có độ tự cảm \(L = \frac{{0,2}}{\pi }{\rm{H}}\). Cảm kháng của đoạn mạch có giá trị là:
-
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại A và B cách nhau 9,6 cm, dao động cùng pha theo phương thẳng đứng. Ở mặt chất lỏng, P là điểm cực tiểu giao thoa cách A và B lần lượt là 15cm và 20cm, giữa P và đường trung trực của đoạn thẳng AB có hai vân giao thoa cực tiểu khác. Số điếm cực đại giao thoa trên đoạn thẳng AP là:
-
Pôlôni \(\;_{84}^{210}{\rm{Po}}\) là chất phóng xạ \(\alpha \) có chu kì bán rã 138 ngày và biến đổi thành hạt nhân chì \(\;_{82}^{206}{\rm{\;Pb}}\). Ban đầu (t=0), một mẫu có khối lượng 105,00 g trong đó 40% khối lượng của mẫu là chất phóng xạ pôlôni \(\;_{84}^{210}{\rm{Po}}\), phần còn lại không có tính phóng xạ. Giả sử toàn bộ các hạt \(\alpha \) sinh ra trong quá trình phóng xạ đều thoát ra khỏi mẫu. Lấy khối lượng của các hạt nhân bằng số khối của chúng tính theo đơn vị u. Tại thời điểm t=552 ngày, khối lượng của mẩu là:
-
Một nguồn phát ra bức xạ đơn sắc với công suất 50mV. Trong một giây nguồn phát ra \(1,3 \cdot {10^{17}}\) phôtôn. Chiếu bức xạ phát ra từ nguồn này vào bề mặt các kim loại: đồng; nhôm; canxi; kali và xesi có giới hạn quang điện lần lượt là: \(0,30\mu {\rm{m}};0,36\mu {\rm{m}};0,43\mu {\rm{m}};0,55\mu {\rm{m}}\) và \(0,58\mu {\rm{m}}\). Lấy \(h = 6,625 \cdot {10^{ - 34}}{\rm{\;J}}.{\rm{s}};c = 3 \cdot {10^8}{\rm{\;m}}/{\rm{s}}\). Số kim loại xảy ra hiện tương quang điện là:
-
Ở một nơi trên mặt đất, hai con lắc đơn có chiều dài l và l+45 (cm) cùng được kích thích để dao động điều hòa. Chọn thời điểm ban đầu là lúc dây treo của hai con lắc đều có phương thẳng đứng. Khi độ lớn góc lệ̣ch dây treo của một con lắc so với phương thẳng đứng là lớn nhất lần thứ ba thì con lắc còn lại ở vị trí có dây treo trùng với phương thẳng đứng lần thứ hai (không tính thời điểm ban đầu). Giá trị của l là:
-
Số nuclôn có trong hạt nhân \(\;_{40}^{90}{\rm{Zr}}\) là:
-
Mạch chọn sóng ở một máy thu thanh là mạch dao động gồm cuộn cảm thuần có độ tự cảm \(50\mu {\rm{H}}\) và tụ điện có điện dung C thay đổi được. Lấy \({\pi ^2} = 10\). Để thu được sóng điện từ có tần số \(10{\rm{MHz}}\) thì giá trị của lúc này là:
-
Một sợi dây mềm có hai đầu cố định. Trên dây đang có sóng dừng và chỉ có một bụng sóng. Sóng truyền trên dây có bước sóng 120cm. Chiều dài của sợi dây là:
-
Theo thuyết lượng tử ánh sáng, mỗi lần một nguyên tử hay phân tử phát xạ ánh sáng thì chúng phát ra
-
Một con lắc đơn có chiều dài l, vật nhỏ khối lượng m, đang dao động điều hòa ở nơi có gia tốc trọng trường g. Khi con lắc đi qua vị trí có li độ cong s thì lực kéo về tác dụng lên vật là:
-
Trên một sợi dây đang có sóng dừng. Hình bên mô tả một phần hình dạng của sợi dây tại hai thời điểm t1 và \({t_2} = {t_1} + 0,8\) (s) (đường nét liền và đường nét đứt). M là một phần tử dây ở điểm bụng.
Tốc độ của M tại các thời điểm t1 và t2 lần lượt là v1 và v2 với \(\frac{{{v_2}}}{{{v_1}}} = \frac{{3\sqrt 6 }}{8}\). Biết tại thời điểm t1 và t2 có vectơ gia tốc đều ngược chiều với chiều chuyển động của nó và trong khoảng thời gian từ t1 đến t2 thì M đạt tốc độ cực đại vmaxmột lần. Giá trị vmax gần nhất với giá trị nào sau đây?
-
Một khung dây dẫn phẳng, kín được đặt trong từ trường đều. Trong khoảng thời gian 0,05s, từ thông qua khung dây tăng đều từ 0 đến 0,02W. Trong khoảng thời gian trên, độ lớn của suất điện động cảm ứng xuất.
-
Một sóng cơ có chu kỳ T, lan truyền trong một môi truờng với tốc độ v. Bước sóng \(\lambda \) được xác định bằng công thức nào sau đây?
-
Một con lắc lò xo đang dao động điều hòa theo phương nằm ngang. Mốc thế năng ở vị trí cân bằng. Khi nói về cơ năng của con lắc, phát biểu nào sau đây sai?
-
Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số góc \(\omega \) thay đổi được vào hai đầu một đoạn mạch gồm điện trở, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Cường độ dòng điện hiệu dụng trong đoạn mạch có giá trị lớn nhất khi
-
Một vật dẫn đang có dòng điện một chiều chạy qua. Trong khoảng thời gian \({\rm{\Delta }}t\), điện lượng dịch chuyển qua tiết diện thẳng của vật dẫn là \({\rm{\Delta }}q\). Cường độ dòng điện I trong vật dẫn được tính bằng công thức nào sau đây?
-
Trong sơ đồ khối của một máy thu thanh vô tuyến đơn giản không có bộ phận nào sau đây?
-
Một vật dao động điều hòa dọc theo trục Ox với phương trình \(x = A{\rm{cos}}\left( {\omega t + \varphi } \right)\). Khi vật đi qua vị trí cân bằng thì độ lớn gia tốc của vật có giá trị là:
