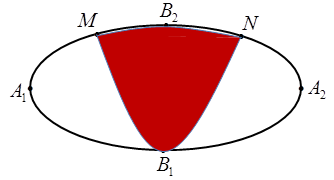
Một biển quảng cáo có dạng Elip với bốn đỉnh \({{A}_{1}},{{A}_{2}},{{B}_{1}},{{B}_{2}}\). như hình vẽ. Người ta chia Elip bởi parapol có đỉnh \({{B}_{1}}\), trục đối xứng \({{B}_{1}}{{B}_{2}}\) và đi qua các điểm M, N.Sau đó sơn phần tô đậm với giá 200.000 đồng/\({{m}^{2}}\) và trang trí đèn led phần còn lại với giá 500.000 đồng/\({{m}^{2}}\).Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết \({{A}_{1}}{{A}_{2}}=4m,{{B}_{1}}{{B}_{2}}=2m,\text{ }MN=2m\).

Cho hàm số \(y=f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \({f}'\left( x \right)=\left( x+2 \right){{\left( x-1 \right)}^{3}}\left( 3-x \right)\). Hàm số đạt cực tiểu tại

Trong không gian Oxyz, cho hai điểm \(M\left( 3;-2;5 \right), N\left( -1;6;-3 \right)\). Mặt cầu đường kính MN có phương trình là:

Cho hàm số y = g(x) có đồ thị như hình vẽ bên.

Hàm số đã cho đồng biến trên khoảng nào sau đây?

Trong không gian Oxyz, cho điểm M(3;2;-1) và mặt phẳng (P):x+z-2=0. Đường thẳng đi qua M và vuông góc với (P) có phương trình là

Hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong \(\left( C \right)\) có phương trình \(y=\frac{1}{4}\,{{x}^{2}}\). Gọi \({{S}_{1}}\,,\,\,{{S}_{2}}\) lần lượt là diện tích của phần không bị gạch và bị gạch như hình vẽ bên dưới. Tỉ số \(\frac{{{S}_{1}}}{{{S}_{2}}}\) bằng

Trong không gian Oxyz, mặt cầu \(\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-8x+2y+1=0\) có tọa độ tâm I và bán kính R lần lượt là

Nghiệm của phương trình \({{2}^{x+1}}=16\) là

Cho số phức \(z=5-2i\). Tìm số phức \(w=iz+\overline{z}\).

Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?

Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SA=2a. Tính theo a thể tích khối chóp S.ABCD.

Cho hình chóp tứ giác đều có cạnh đáy bằng 2a, cạnh bên bằng 3a. Gọi \(\alpha \) là góc giữa mặt bên và mặt đáy, mệnh đề nào dưới đây đúng?

Trong không gian Oxyz, cho đường thẳng \(d:\,\frac{x+3}{2}=\frac{y+1}{1}=\frac{z}{-1}\) và mặt phẳng \(\left( P \right):\,x+y-3z-2=0\). Gọi d' là đường thẳng nằm trong mặt phẳng \(\left( P \right)\), cắt và vuông góc với d. Đường thẳng d' có phương trình là

Trong không gian Oxyz, cho điểm \(M\left( -3\ ;\ -2\ ;\ 1 \right)\). Hình chiếu vuông góc của điểm M lên mặt phẳng \(\left( Oxy \right)\) là điểm:

Rút gọn biểu thức \(P=\frac{{{a}^{\sqrt{3}+1}}.{{a}^{2-\sqrt{3}}}}{{{\left( {{a}^{\sqrt{2}-2}} \right)}^{\sqrt{2}+2}}}\) với a>0

Điểm \(A\) trong hình bên dưới là điểm biểu diễn số phức \(z\).

Mệnh đề nào dưới đây đúng?

Tổng các nghiệm của phương trình \({{\log }_{\frac{1}{2}}}\left( {{x}^{2}}-5x+7 \right)=0\) bằng

Cho số phức \(z={{(1-2i)}^{2}}\). Tính mô đun của số phức \(\frac{1}{z}\).

Cho hàm số có \({f}'\left( x \right)\) và \({f}''\left( x \right)\) liên tục trên \(\mathbb{R}\). Biết \({f}'\left( 2 \right)=4\) và \({f}'\left( -1 \right)=-2,\) tính \(\int\limits_{-1}^{2}{{f}''\left( x \right)\text{d}x}\)

Giá trị nhỏ nhất của hàm số \(y={{x}^{3}}-2{{x}^{2}}-4x+5\) trên đoạn \(\left[ 1\,;\,3 \right]\) bằng

Cho cấp số cộng \(\left( {{u}_{n}} \right)\) có số hạng đầu \({{u}_{1}}=2\) và công sai d=5. Giá trị của \({{u}_{5}}\) bằng