Cho mạch điện như hình vẽ. Đặt vào hai đầu A, B một điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Điều chỉnh C để tổng điện áp hiệu dụng UAM + UMB lớn nhất thì tổng đó bằng 2U và khi đó công suất tiêu thụ của đoạn mạch AM là 36 W. Tiếp tục điều chỉnh C để công suất tiêu thụ của đoạn mạch lớn nhất thì công suất lớn nhất đó bằng
.png)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai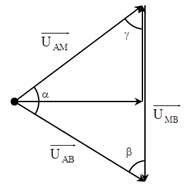
+ Biểu diễn vecto các điện áp.
+ Áp dụng định lý sin trong tam giác, ta có:
\(\frac{{{U}_{AM}}}{\sin \beta }=\frac{{{U}_{MB}}}{\sin \alpha }=\frac{{{U}_{AB}}}{\sin \gamma }=\frac{{{U}_{AM}}+{{U}_{MB}}}{\sin \alpha +\sin \beta }\to {{U}_{AM}}+{{U}_{MB}}=\frac{{{U}_{AB}}}{\sin \gamma }\left( \sin \alpha +\sin \beta \right)\)
với \(\gamma \) luôn không đổi.
\({{U}_{AM}}+{{U}_{MB}}=\frac{2{{U}_{AB}}}{\sin \gamma }\sin \left( \frac{\alpha +\beta }{2} \right)\cos \left( \frac{\alpha -\beta }{2} \right)=\frac{2{{U}_{AB}}}{\sin \gamma }\sin \left( \frac{180-\gamma }{2} \right)c\text{os}\left( \frac{\alpha \text{-}\beta }{\text{2}} \right)\)
\(\to {{\left( {{U}_{AM}}+{{U}_{MB}} \right)}_{\max }}\) khi \(\alpha =\beta .\)
=> \({{\left( {{U}_{AM}}+{{U}_{MB}} \right)}_{\max }}=\frac{2U}{\sin \gamma }\sin \left( \frac{180-\gamma }{2} \right)=2U\to \gamma =60{}^\circ .\)
\(\to \) Các vecto hợp với nhau thành tam giác đều \(\to \) khi xảy ra cực đại u chậm pha hơn i một góc \(30{}^\circ \).
\(P={{P}_{\max }}{{\cos }^{2}}\varphi \to {{P}_{\max }}=\frac{P}{{{\cos }^{2}}\varphi }=\frac{36}{{{\cos }^{2}}30{}^\circ }=48\,\,W.\)
Câu hỏi liên quan
-
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn S phát ra ba ánh sáng đơn sắc: 0,42μm(màu tím); 0,56μm (màu lục); 0,70μm (màu đỏ). Số vân tím, vân lục và vân đỏ nằm giữa hai vân sáng liên tiếp có màu giống như màu của vân trung tâm là:
-
Kim loại làm catốt của một tế bào quang điện có giới hạn quang điện là λo. Chiếu lần lượt tới bề mặt catốt hai bức xạ có bước sóng λ1 = 0,4 μm và λ2 = 0,5 μm thì vận tốc ban đầu cực đại của các electron bắn ra khác nhau 1,5 lần. Bước sóng λo là
-
Hai sóng cùng tần số, được gọi là sóng kết hợp, nếu có
-
Hai dao động điều hòa có đồ thị li độ - thời gian như hình vẽ. Tổng vận tốc tức thời của hai dao động có giá trị lớn nhất là
.png)
-
Một vật dao động điểu hòa khi đang chuyển động từ vị trí cân bằng đến vị trí biên âm thì
-
Lần lượt chiếu hai bức xạ có bước sóng λ1 = 0,75 μm và λ2 = 0,25 μm vào một tấm kẽm có giới hạn quang điện λo = 0,35 μm. Bức xạ nào gây ra hiện tượng quang điện ?
-
Đặt vào hai đầu mạch điện chỉ có cuộn thuần cảm một điện áp xoay chiều \(u={{U}_{0}}\cos \left( 100\pi t-\frac{\pi }{2} \right)V\).Pha ban đầu của cường độ dòng điện trong mạch bằng
-
Có 100 (g) chất phóng xạ với chu kì bán rã là 7 ngày đêm. Sau 28 ngày đêm khối lượng chất phóng xạ đó còn lại là
-
Quang phổ Mặt Trời được máy quang phổ ghi được là:
-
Cho một mạch điện có suất điện động của bộ nguồn ξ=30V . Dòng điện chạy trong mạch là I=3A .Hiệu điện thế trên hai cực của bộ nguồn là U=18V.Điện trở R của mạch ngoài và điện trở trong r của bộ nguồn là :
-
Một đoạn mạch xoay chiều gồm cuộn dây thuần cảm L = 1/p (H) mắc nối tiếp với R = 100W. Hiệu điện thế ở hai đầu mạch là u = 100\(\sqrt{2}\)sin100pt (V). Biểu thức cường độ dòng điện trong mạch là
-
Trên vỏ của một acquy có ghi 12V, điện trở trong của acquy là 0,06\(\Omega \). Mắc vào hai cực của acquy một bóng đèn có ghi 12V – 5W. Khi đó, cường độ dòng điện chạy qua đèn là
-
Trong thí nghiệm Y-âng, hai khe được chiếu bằng ánh sáng trắng ( có bước sóng từ 0,4μm đến 0,6 μm ). Khi đó tại vị trí của vân sáng bậc 4 của ánh sáng đỏ ( λ = 0,76 μm ) còn có bao nhiêu bức xạ đơn sắc cho vân sáng tại đó ?
-
Đặt vào hai đầu đoạn mạch RLC nối tiếp một hiệu điện thế xoay chiều u = Uo sinωt thì độ lệch pha của hiệu điện thế u với cường độ dòng điện i trong mạch được tính theo công thức
-
Cho ba điện tích q1= 4µC, q2= 16µC, q3 = - 64µC lần lượt đặt tại ba điểm A,B,C thẳng hàng( trong chân không). Biết AB=20cm, BC=60cm. Lực điện tổng hợp tác dụng lên điện tích q1 bằng:
-
Trường hợp nào sao đây là biểu hiện của “ từ trường “ ?
-
Sóng (cơ học) ngang:
-
Trong quá trình truyền tải điện năng biện pháp giảm hao phí trên đường dây tải điện được sử dụng chủ yếu hiện nay là
-
Phát biểu nào sau đây là đúng khi nói về phản ứng hạt nhân?
-
Tia tử ngoại không có tác dụng nào say đây?
