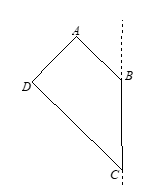
Cho hình thang ABCD vuông tại A và D có \(CD=2AB=2AD=6.\) Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quay xung quanh đường thẳng BC?

 

Cho đồ thị \(\left( C \right):y=\frac{x+2}{x-1}\). Gọi \(A,\ B,\ C\) là 3 điểm phân biệt thuộc \(\left( C \right)\) sao cho trực tâm \(H\) của tam giác \(ABC\) thuộc đường thẳng \(\Delta :y=-3x+10\). Độ dài đoạn thẳng \(OH\) bằng?

Cho hình chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(2a\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy và \(SA=3\sqrt{2}a\). Tính thể tích của khối chóp \(S.ABCD\)?

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB=3,\,AD=4\) và các cạnh bên của hình chóp tạo với mặt đáy góc \(60{}^\circ \). Tính thể tích khối cầu ngoại tiếp hình chóp đã cho?

Tính thể tích của khối chóp có diện tích đáy \(B=6\) và chiều cao \(h=4\) là?

Với các số \(a,\ b>0\) thỏa mãn \({{a}^{2}}+{{b}^{2}}=7ab\), giá trị biểu thức \({{\log }_{3}}\left( a+b \right)\) bằng?

Hàm số nào bên dưới đây không có cực trị?

Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số sau \(y=\left| 3{{x}^{4}}-m{{x}^{3}}+6{{x}^{2}}+m-3 \right|\) đồng biến trên khoảng \(\left( 0;+\infty  \right)\)?

Có tất cả bao nhiêu số nguyên dương của tham số m để hàm số sau \(y=\frac{\cos x+1}{10\cos x+m}\) đồng biến trên khoảng \(\left( 0;\frac{\pi }{2} \right)\cdot \)?

Cho có tháp nước như hình, tháp được thiết kế gồm thân tháp có dạng hình trụ, phần mái phía trên dạng hình nón và đáy là nửa hình cầu. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hình nón đều bằng 3m, chiều cao hình trụ là 2m, chiều cao của hình nón là 1m. Thể tích của toán bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?

Cho \(x,y>0\) và \(\alpha ,\beta \in \mathbb{R}\). Tìm đẳng thức sai?

Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác vuông cân tại \(B\) và \(AC=2a\). Hình chiếu vuông góc của \({A}'\) trên mp \(\left( ABC \right)\) là trung điểm \(H\) của cạnh \(AB\) và \(A{A}'=a\sqrt{2}\). Tính thể tích \(V\) của khối lăng trụ đã cho?

Một hộp có 6 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ 3 màu và số viên bi đỏ lớn hơn số viên bi vàng?

Tổng số đường tiệm cận đứng và ngang của ĐTHS \(y=\frac{\sqrt{1-{{x}^{2}}}}{{{x}^{2}}+2x}\) là?

Có tất cả bao nhiêu cặp số nguyên \(\left( x;y \right)\) thỏa mãn \(0\le x\le 4000\) và \(5\left( {{25}^{y}}+2y \right)=x+{{\log }_{5}}{{\left( x+1 \right)}^{5}}-4\)?

Gọi \(M,m\) lần lượt là GTLN, GTNN của hàm số \(y={{x}^{3}}-3{{x}^{2}}-9x-1\) trên đoạn\(\left[ 1;5 \right]\). Tính giá trị \(T=2M-m\)?

Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình?

Cho phương trình sau \(\left( 4\log _{2}^{2}x+{{\log }_{2}}x-5 \right)\sqrt{{{7}^{x}}-m}=0\) (\(m\) là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của  để phương trình đã cho có đúng 2 nghiệm phân biệt?

Cho hàm số \(y=\frac{ax+b}{cx-1}\) có đồ thị như hình. Giá trị của tổng \(S=a+b+c\) bằng?

Cho hình chóp \(S.ABC\) có \(AB=4a,BC=3\sqrt{2}a,\) \(\widehat{ABC}=45{}^\circ ;\widehat{SAC}=\widehat{SBC}=90{}^\circ \); Sin góc giữa 2 mặt phẳng\(\left( SAB \right)\) và \(\left( SBC \right)\) bằng \(\frac{\sqrt{2}}{4}.\) Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng?

Tích tất cả các nghiệm của phương trình \(\log _{3}^{2}x-2{{\log }_{3}}x-7=0\) là?