Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai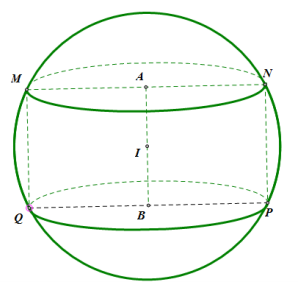
Giả sử hình cầu có tâm là I và có bán kính là R, khối trụ có tâm của hai đáy là A, B.
Gọi r h, là bán kính và chiều cao của khối trụ\((0<h=2 I A<2 R)\)
\(r=\sqrt{R^{2}-A I^{2}}=\sqrt{R^{2}-\frac{h^{2}}{4}}\)
Thể tích khối trụ là \(V=\pi r^{2} h=\pi\left(R^{2}-\frac{h^{2}}{4}\right) h=\pi\left(R^{2} h-\frac{h^{3}}{4}\right)\)
Xét hàm số \(f(h)=R^{2} h-\frac{h^{3}}{4} \text { vói } 0<h<2 R\)
\(f^{\prime}(h)=R^{2}-\frac{3}{4} h^{2} ; f^{\prime}(h)=0\)
\(\Leftrightarrow h=\frac{2 \sqrt{3}}{3} R\)
Bảng biến thiên
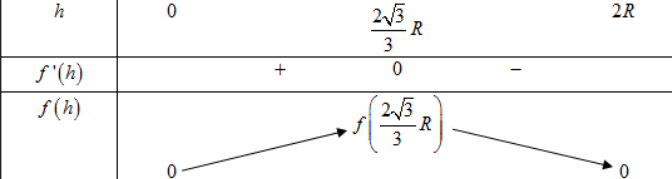
Dựa vào bảng biến thiên ta thấy thể tích của khối trụ lớn nhất khi và chỉ khi \(h=\frac{2 \sqrt{3}}{3} R\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Trần Phú lần 2
Câu hỏi liên quan
-
Cho (H ) là hình phẳng giới hạn bởi \((C): y=\sqrt{x}, y=x-2\) và trục hoành (hình vẽ). Diện tích của (H ) bằng
-
Cho hàm số \(y=\frac{-x+1}{2 x-1}(C), y=x+m\). Với mọi m đường thẳng ( d) luôn cắt đồ thị (C) tại hai điểm phân biệt A và B . Gọi \(k_{1} ; k_{2}\) , lần lượt là hệ số góc của các tiếp tuyến với (C) tại A và B . Giá trị nhỏ nhất của \(T=k_{1}^{2020}+k_{2}^{2020}\) bằng
-
Cho hình chóp tứ giác \(S . A B C D\) . có đáy ABCD là hình vuông cạnh bằng a , \(S A \perp(A B C)\), SA= 3a . Thể tích V của khối chóp \(S . A B C D\) . là
-
Cho hàm số ff(x) liên tục trên \(\mathbb{R} \text { và } f(2)=16, \int\limits_{0}^{2} f(x) d x=4\) . Tính \(I=\int_{0}^{4} x f^{\prime}\left(\frac{x}{2}\right) \mathrm{d} x\)
-
Tìm tập xác định D của hàm số \(y=\left(x^{2}-2 x+1\right)^{\frac{1}{3}}\)
-
Cho hình chóp \(S . A B C \text { có } S A=S B=S C=4, A B=B C=C A=3\). Tính thể tích khối nón giới hạn bởi hình nón có đỉnh là S và đáy là đường tròn ngoại tiếp ∆ABC .
-
Tích phân \(I=\int_{0}^{1} \mathrm{e}^{x+1} \mathrm{d} x\) bằng
-
Cho hàm số y =f(x) có bảng biến thiên của đạo hàm y ' như sau:
Bất phương trình \(f(x)<\mathrm{e}^{x}+m\) đúng với mọi \(x \in(-1 ; 1)\)khi và chỉ khi
-
Phương trình đường tiệm cận ngang của đồ thị hàm số \(y=\frac{2 x-6}{x+1}\) là
-
Gọi R là bán kính, S là diện tích mặt cầu và V là thể tích của khối cầu. Công thức nào sau đây sai?
-
Họ nguyên hàm của hàm số \(f(x)=5 x^{4}+2\) là:
-
Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm \(A(1 ; 1 ; 2), B(2 ;-1 ; 3)\) . Viết phương trình đường thẳng AB .
-
Số nào trong các số sau là số thuần ảo?
-
Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số dưới đây?
-
Cho hàm số y = f(x) liên tục, nhận giá trị dương trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình vẽ bên dưới:
Hàm số \(y=\log _{2}(f(2 x))\) đồng biến trên khoảng nào trong các khoảng sau:
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime} \text { cạnh } 2 a\) . Gọi M là trung điểm của BB′ và P thuộc cạnh DD′ sao cho \(D P=\frac{1}{4} D D^{\prime}\). Biết mặt phẳng ( AMP) cắt CC′ tại N , thể tích của khối đa diện AMNPBCD bằng
-
Mô đun của số phức\(z=12-5 i\) là
-
Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng
-
Giá trị nhỏ nhất của hàm số \(y=\frac{-x^{2}+x-6}{x+1}\) trên đoạn [0;3] bằng
-
Cho \(a, b, c\) là các số thực dương, a khác 1. Tìm mệnh đề sai trong các mệnh đề sau:
