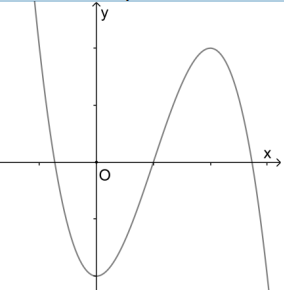
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime} \text { cạnh } 2 a\) . Gọi M là trung điểm của BB′ và P thuộc cạnh DD′ sao cho \(D P=\frac{1}{4} D D^{\prime}\). Biết mặt phẳng ( AMP) cắt CC′ tại N , thể tích của khối đa diện AMNPBCD bằng
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai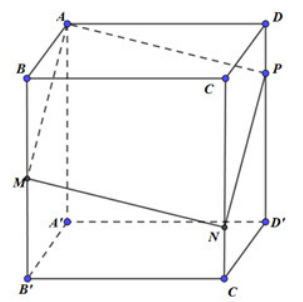
Thể tích khối lập phương là \(V=8 a^{3}\)
Ta có: \(a=\frac{A A}{A A^{\prime}}=0, b=\frac{B M}{B B^{\prime}}=\frac{1}{2}, \quad c=\frac{C N}{C C^{\prime}}, d=\frac{D P}{D D^{\prime}}=\frac{1}{4}\)
Vì A, M, N, P đồng phẳng nên
Khi đó \(\frac{V_{A M N P B C D}}{V_{A B C D . A^{\prime} B^{\prime} C D^{\prime}}}=\frac{1}{4}(a+b+c+d)=\frac{1}{4}\left(0+\frac{1}{2}+\frac{3}{4}+\frac{1}{2}\right)=\frac{3}{8}\)
Vậy \(\Rightarrow V_{A M N P B C D}=\frac{3}{8} \cdot V_{A B C D . A^{\prime} B^{\prime} C D^{\prime}}=3 a^{3}\)
Đề thi thử tốt nghiệp THPT QG môn Toán năm 2020
Trường THPT Chuyên Trần Phú lần 2
Câu hỏi liên quan
-
Cho hàm số ff(x) liên tục trên \(\mathbb{R} \text { và } f(2)=16, \int\limits_{0}^{2} f(x) d x=4\) . Tính \(I=\int_{0}^{4} x f^{\prime}\left(\frac{x}{2}\right) \mathrm{d} x\)
-
Giá trị nhỏ nhất của hàm số \(y=\frac{-x^{2}+x-6}{x+1}\) trên đoạn [0;3] bằng
-
Một người lập kế hoạch gửi tiết kiệm ngân hàng như sau: Đầu tháng 1 năm 2019, người đó gửi 10 triệu đồng; sau mỗi đầu tháng tiếp theo, người đó gửi số tiền nhiều hơn 10% so với số tiền đã gửi ở tháng liền trước đó. Biết rằng lãi suất ngân hàng không đổi là 0,5% mỗi tháng và được tính theo hình thức lãi kép. Với kế hoạch như vậy, đến hết tháng 12 năm 2020, số tiền của người đó trong tài khoản tiết kiệm là bao nhiêu? (Làm tròn đến hàng nghìn)
-
Đường cong trong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số dưới đây?
-
Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính R là
-
Cho hàm số \(y=x^{3}-3 x^{2}+2\). Đồ thị hàm số có điểm cực đại là
-
Cho hàm số y = f(x)xác định trên \(\mathbb{R} \backslash\{1\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ:
Hàm số \(y=|f(x)|\)có bao nhiêu điểm cực trị?
-
Trong không gian với hệ trục tọa độ Oxyz , cho hai điểm \(A(1 ; 1 ; 2), B(2 ;-1 ; 3)\) . Viết phương trình đường thẳng AB .
-
Cho hàm số y = f(x) liên tục, nhận giá trị dương trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình vẽ bên dưới:
Hàm số \(y=\log _{2}(f(2 x))\) đồng biến trên khoảng nào trong các khoảng sau:
-
Trong không gian với hệ trục tọa độ Oxyz , cho mặt cầu \((S): x^{2}+y^{2}+z^{2}+4 x-2 y+6 z+5=0\) . Mặt cầu (S ) có bán kính là
-
Từ các chữ số 1,5,6,7 có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau?
-
Mô đun của số phức\(z=12-5 i\) là
-
Số nào trong các số sau là số thuần ảo?
-
Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a . Thể tích của khối nón đã cho bằng
-
Cho số phức z thỏa mãn điều kiện \((1+i) \bar{z}-1-3 i=0\) . Tìm phần ảo của số phức
-
Đồ thị sau là đồ thị của hàm số nào trong bốn hàm số cho dưới đây?
-
Ông A muốn sau 5 năm có 1.000.000.000 đồng để mua ô tô Camry. Biết lãi suất hàng tháng là 0,5% , tiền lãi sinh ra hàng tháng được nhập vào tiền vốn và số tiền gửi hàng tháng là như nhau. Hỏi rằng ông A phải gửi ngân hàng mỗi tháng số tiền gần nhất với số tiền nào sau đây?
-
Cho hàm số y = f(x) có bảng biến thiên như sau:
Tập hợp tất cả các giá trị thực của tham số m để phương trình \(f(x)+m=0\) có hai nghiệm phân biệt là
-
Giải bất phương trình \((7+4 \sqrt{3})^{x-1}<7-4 \sqrt{3}\)
-
Cho hình lăng trụ đứng \(A B C D \cdot A^{\prime} B^{\prime} C D^{\prime}\) có \(A A^{\prime}=3 a, A C=4 a, B D=5 a\) , ABCD là hình thoi. Thể tích của khối lăng trụ \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) bằng
