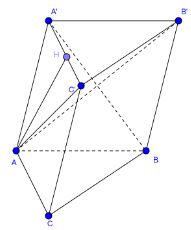
Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Biết AC’ tạo với mặt phẳng (A'B'C) một góc 600 và AC' = 4a. Tính thể tích V của khối đa diện ABCB’C’.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Ta có:
\({V_{A.A'B'C'}} + {V_{A.BCC'B'}} = {V_{ABC.A'B'C'}}\)
\(\begin{array}{l}
\Rightarrow {V_{A.BCC'B'}} = {V_{ABC.A'B'C'}} - \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{3}.{V_{ABC.A'B'C'}}
\end{array}\)
\(= \frac{2}{3}{V_{ABC.A'B'C'}}\)
Gọi H là hình chiếu của A trên mặt phẳng
\(\Rightarrow \widehat {\left( {AC';\left( {A'B'C'} \right)} \right)}= \widehat {AC'H} = {60^0}\)
Khi đó
\(\sin \widehat {AC'H} = \frac{{AH}}{{AC'}} \)
\(\Rightarrow AH = \sin {60^0}.4a = 2a\sqrt 3\)
\(\Rightarrow {V_{ABC.A'B'C'}} = AH.{S_{\Delta A'B'C'}}\)
\(= 2a\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}}}{2}\)
Vậy thể tích của khối đa diện cần tìm là:
\({V_{A.BCC'B'}} = \frac{2}{3}.{V_{ABC.A'B'C'}}\)
\(= \frac{2}{3}.\frac{{3{a^3}}}{2} = {a^3}\).
Đề thi giữa HK1 môn Toán 12 năm 2022-2023
Trường THPT Trần Hưng Đạo
Câu hỏi liên quan
-
Tìm giá trị lớn nhất M của hàm số \(y = \cos 2x + 4\cos x + 1.\)
-
Một kim tự tháp ở Ai Cập được xây dựng vào khoảng 2500 trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 150 m, cạnh đáy dài 220 m. Tính diện tích xung quanh S của kim tự tháp này.
-
Tìm giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} - 9x + 6\) trên \(\left[ { - 4;4} \right]\).
-
Cho hình chóp S.ABC có đáy là tam giác vuông cân có cạnh huyền là 4a và thể tích bằng \(a^3\). Tính chiều cao h của khối chóp S.ABC.
-
Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x - 1}}{{2x - 1}}?\)
-
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SD = \frac{{a\sqrt {17} }}{2}\), hình chiếu vuông góc H của S lên mặt (ABCD) là trung điểm của đoạn AB. Tính chiều cao h của khối chóp H.SBD theo a.
-
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích bằng 1. Trên cạnh SC lấy điểm E sao cho SE=2EC. Tính thể tích V của khối tứ diện SEBD.
-
Khối đa diện đều có 12 mặt thì có bao nhiêu cạnh?
-
Hàm số y = x3 – 3x2 + 4 có đồ thị (C). Tiếp tuyến của (C) song song với đường thẳng y = –3x có phương trình là
-
Tìm tất cả các điểm cực đại của hàm số \(y = - {x^4} + 2{x^2} + 1.\)
-
Cho hàm số y = x3 + x + 1 có đồ thị (C). Tìm câu trả lời sai
-
Trong các hàm số sau, hàm số nào có cực đại, cực tiểu và xCT < xCĐ.
-
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình \({x^3} + {x^2} + x = m{\left( {{x^2} + 1} \right)^2}\) có nghiệm thuộc đoạn [0;1].
-
Hàm số y = f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây là đúng?
-
Cho hàm số \(y = {x^2}(3 - x).\) Mệnh đề nào sau đây là đúng?
-
Gọi A và B là hai điểm cực trị của đồ thị hàm số \(f\left( x \right) = {x^3} - 3x + 1.\) Tính độ dài AB.
-
Cho hàm số \(y = \frac{x}{{x - 1}}.\) Mệnh đề nào sau đây là đúng?
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết hình chóp S.ABC có thể tích bằng \(a^3\). Tính khoảng cách d từ điểm A đến mặt phẳng (SBC).
-
Tìm tất cả các giá trị nguyên của tham số thực m để hàm số \(y = \frac{1}{3}{x^3} + \frac{1}{2}m{x^2}\) có điểm cực đại x1 điểm cực tiểu x2 sao cho \(- 2 < {x_1} < - 1;\,\,1 < {x_2} < 2.\)
-
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\) biết \(f'\left( x \right) = x{\left( {x - 1} \right)^2}.\) Khẳng định nào sau đây là
