ADMICRO
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy, AB=2a,^BAC=600 và SA=a√2. Góc giữa đường thẳng SB và mặt phẳng (SAC) bằng?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ADSENSE / 21
Chủ đề: Đề thi Học Kỳ/Giữa Kỳ
Môn: Toán Lớp 12
Lời giải:
Báo sai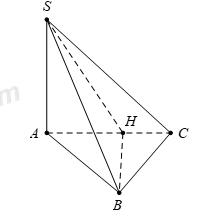
Kẻ BH⊥AC(H∈AC)⇒BH⊥(SAC)
Suy ra ^SB;(SAC)=^(SB;SH)=^BSH.
Tam giác ABH vuông tại H, có sin^BAH=BHAB⇒BH=a√3.
Tam giác SAB vuông tại A, có SB=√SA2+AB2=a√6.
Do đó SB=√2BH⇒ΔABH vuông cân tại H⇒^BSH=450.
Chọn B.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi giữa HK1 môn Toán 12 năm 2023-2024
Trường THPT Nguyễn Thị Minh Khai
25/03/2025
416 lượt thi
0/40
Bắt đầu thi
ZUNIA12
ZUNIA9
AANETWORK