Với giá trị nào của tham số m thì phương trình \(x+\sqrt{4-x^{2}}=m\) có nghiệm?
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTXĐ: \(D=[-2 ; 2]\)
Phương trình \(x+\sqrt{4-x^{2}}=m\) có nghiệm khi đường thẳng y = m cắt đồ thị của hàm số \(y=x+\sqrt{4-x^{2}}(1)\)
Xét hàm số \(y=x+\sqrt{4-x^{2}} \text { trên } D=[-2 ; 2]\)
\(y^{\prime}=1-\frac{x}{\sqrt{4-x^{2}}}\)
Cho \(y^{\prime}=0 \Leftrightarrow 1-\frac{x}{\sqrt{4-x^{2}}}=0 \Leftrightarrow \sqrt{4-x^{2}}=x \Leftrightarrow\left\{\begin{array}{l} x \geq 0 \\ 4-x^{2}=x^{2} \end{array} \Rightarrow x=\sqrt{2}\right.\)
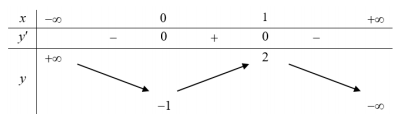
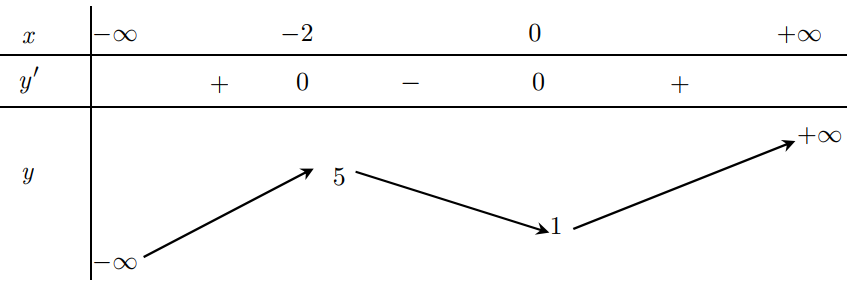
Từ bảng biến thiên ta thấy đường thẳng y = m cắt đồ thị hàm số (C) khi \(-2 \leq m \leq 2 \sqrt{2}\)
Câu hỏi liên quan
-
Cho hàm số \(y=2{x^3} - 3\left( {m + 1} \right){x^2} + 6\left( {m + 1} \right)2x + 1\). Hình nào dưới đây mô tả chính xác nhất đồ thị hàm số trên?
-
Đồ thị hàm số \(y = \sqrt {{{\sin }^2}x + 4} \) cắt trục tung tại điểm có tung độ bằng
-
Tìm giá trị lớn nhất của tham số m sao cho bất phương trình \(2^{\cos ^{2} x}+3^{\sin ^{2} x} \geq m \cdot 3^{\cos ^{2} x}\) có nghiệm?
-
Tất cả giá trị của tham số m để phương trình \({x^4} – 2{x^2} – m + 3 = 0\) có hai nghiệm phân biệt là
-
Cho hàm số f(x)=2mx+lnx. Tìm mm để nguyên hàm F(x) của f(x) thỏa mãn F(1) = 0 và F(2) = 2 + 2ln2
-
Cho hàm số \(y = \frac{{x + 2}}{{2x + 3}}\left( 1 \right)\). Viết phương trình tiếp tuyến của đồ thị hàm số đã cho, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A; B và tam giác OAB cân tại gốc tọa độ.
-
Cho hàm số y = f(x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị hàm số y = f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
-
Đồ thị hàm số \(y = {x^2} – \left| x \right| + 1\) cắt trục tung tại điểm có tung độ bằng
-
Biết rằng đồ thị hàm số \(y = \frac{{x + 3}}{{x - 1}}\) và đường thẳng y = x – 2 cắt nhau tại hai điểm phân biệt A(xA;yA) và B(xB;yB). Tính yA + yB.
-
Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số dưới đâ?
-
Hàm số \(y = {x^4} + \left( {{m^2} - 4} \right){x^2} + 5\) có ba cực trị khi:
-
Bảng biến thiên dưới đây là của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
-
Hàm số y = f(x) xác định, liên tục trên khoảng K và có đạo hàm f′(x) trên K. Biết hình vẽ sau đây là của đồ thị hàm số f′(x) trên K.
.png)
Khẳng định nào sau đây là đúng?
-
Cho đồ thị hàm số y=f(x) có đồ thị như hình vẽ. Tìm số nghiệm của phương trình f(x)=x
-
Tìm tất cả các điểm thuộc đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaaGOmaiaadIhacqGHRaWkcaaIXaaabaGaamiEaiab % gkHiTiaaigdaaaaaaa!3E03! y = \frac{{2x + 1}}{{x - 1}}\) có khoảng cách đến trục hoành bằng 1
-
Cho hàm số \(y = \frac{3}{{x + 1}}\) có đồ thị (C). Mệnh đề nào sau đây là mệnh đề sai?
-
:Cho hàm số y=f(x) có bảng biến thiên như sau
Số nghiệm của phương trình \(f(2-x)-1=0\) là
-
Giao điểm giữa đồ thị \((C):y = \frac{{{x^2} – 2x – 3}}{{x – 1}}\) và đường thẳng \(\left( d \right):y = x + 1\) là
-
Hàm số y = - x3 + 3x2 – 1 là đồ thị nào sau đây
-
Có bao nhiêu điểm M thuộc đồ thị hàm số \(y = \frac{{x + 2}}{{x - 1}}\) sao cho khoảng cách từ M đến trục tung bằng hai lần khoảng cách từ M đến trục hoành
