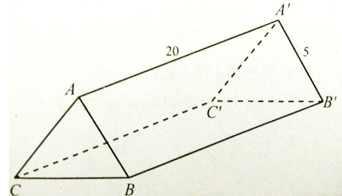
Một hành lang giữa hai tòa tháp có hình dạng một hình lăng trụ đứng. Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Với độ dài xấp xỉ nào của BC thì thể tích hành lang này lớn nhất
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiThể tích hình lăng lớn nhất khi và chỉ khi diện tích ΔABC lớn nhất.
Gọi độ dài BC là x (m). Kẻ AH ⊥ BC.
\(AH = \sqrt {25 - \frac{{{x^2}}}{4}} \Rightarrow {S_{ABC}} = \frac{x}{2}\sqrt {25 - \frac{{{x^2}}}{4}} = \frac{{x\sqrt {100 - {x^2}} }}{4}\)
Bài toán đưa về tìm x ∈ (0; 10) để hàm số \(y = x\sqrt {100 - {x^2}} \) có giá trị lớn nhất.
Ta có:
\(y' = 1.\sqrt {100 - {x^2}} + x.\frac{{ - x}}{{\sqrt {100 - {x^2}} }} = \frac{{100 - 2{x^2}}}{{\sqrt {100 - {x^2}} }}\)
y' xác định \(\forall x \in \left( {0;10} \right)\)
\(y' = 0 \Rightarrow x = 5\sqrt 2 \)
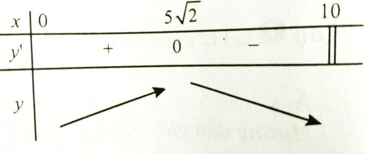
Bảng biến thiên:
Hàm số đạt giá trị lớn nhất tại \(x\; = \;5\sqrt 2 \; \approx \;7\)