ADMICRO
Giá trị lớn nhất của hàm số \( y = \frac{1}{{{x^2} + x + 1}}\) trên khoảng (−∞;+∞):
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Môn: Toán Lớp 12
ZUNIA12
Lời giải:
Báo saiTa có:
\( y' = \frac{{ - 2x - 1}}{{{{\left( {{x^2} + x + 1} \right)}^2}}} = 0 \Leftrightarrow x = - \frac{1}{2}\)
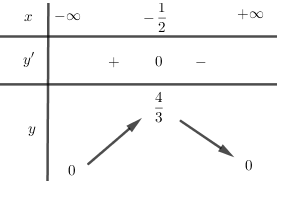
Bảng biến thiên:
Từ bảng biến thiên ta thấy, hàm số đạt GTLN \( \mathop {\max }\limits_{\left( { - \infty ; + \infty } \right)} y = \frac{4}{3} \Leftrightarrow x = - \frac{1}{2}\)
ZUNIA9
AANETWORK



.jpg.png)
.jpg.png)