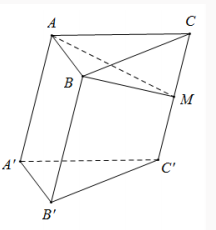
Cho hình lăng trụ ABC.A’B’C’ vì M là trung điểm của CC’. Gọi khối đa diện (H) là phần còn lại của khối lăng trụ ABC.A’B’C’ sau khi cắt bỏ đi khối chóp M.ABC. Tính tỷ số thể tích của (H) và khối chóp M.ABC.
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi V là thể tích khối chóp M.ABC.
M là trung điểm của CC’
Theo bài ra ta có:\(\begin{array}{l} \frac{{{V_{C'ABM}}}}{{{V_{C'ABC}}}} = \frac{{C'M}}{{C'C}} = \frac{1}{2} \Rightarrow {V_{C'ABM}} = \frac{1}{2}{V_{C'ABC}}\\ \Rightarrow {V_{C'ABM}} = {V_{M.ABC}} = \frac{1}{2}{V_{C'ABC}} = V \Rightarrow {V_{C'ABC}} = 2V \end{array}\)Ta lại có \(\begin{array}{l} {V_{C'ABC}} = {V_{AA'B'C'}} = {V_{BA'B'C'}} = 2V\\ \to {V_{\left( H \right)}} = {V_{C'ABC}} + {V_{AA'B'C'}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} + {V_{BA'B'C'}} - {V_{MABC}} = 5V\\ \to \frac{{\left( H \right)}}{{{V_{M.ABC}}}} = 5 \end{array}\)



.png)











