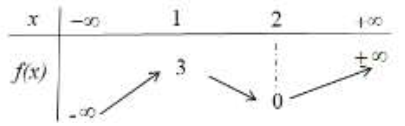
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên dưới. Hỏi có tất cả bao nhiêu giá trị thực của tham số m để hàm số \(g\left( x \right) = {x^2} – 2{m^2}x + {m^4} – f\left( {f\left( x \right)} \right)\) đạt giá trị nhỏ nhất ?
.jpg.png)
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiNhận thấy \(\max f\left( x \right) = f\left( { – 3} \right) \Leftrightarrow f\left( x \right) \le f\left( { – 3} \right) \Leftrightarrow – f\left( x \right) \ge – f\left( { – 3} \right), \forall x \in \mathbb{R}\).
Lại có \( – f\left( {f\left( x \right)} \right) \le – f\left( { – 3} \right), \forall x \in \mathbb{R}\).
\(g\left( x \right) = {x^2} – 2{m^2}x + {m^4} – f\left( {f\left( x \right)} \right) = {\left( {x – {m^2}} \right)^2} – f\left( {f\left( x \right)} \right) \ge 0 – f\left( { – 3} \right) = – f\left( { – 3} \right)\).
Dấu bằng xảy ra khi \(\left\{ \begin{array}{l}f\left( {f\left( x \right)} \right) = f\left( { – 3} \right)\\x = {m^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}f\left( x \right) = – 3 \Leftrightarrow \left[ \begin{array}{l}x = {x_1} < 0{\rm{ }}\left( {loai} \right)\\x = {x_2} > 0\\x = {x_3} > 0\\x = {x_4} > 0\end{array} \right.\\m = \pm \sqrt x \end{array} \right.\).
Vậy có tất cả 6 giá trị m thỏa mãn yêu cầu bài toán.
Câu hỏi liên quan
-
Hàm số \(y=\sin ^{2} x+2\) có giá trị nhỏ nhất, giá trị lớn nhất lần lượt bằng
-
Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\sqrt{x-x^{2}} ?\)
-
Hàm số y = x8 + (x4 – 1) 2 + 5 đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [0;2] lần lượt tại hai điểm có hoành độ x1; x2. Khi đó tích x1.x2 có giá trị bằng:
-
Cho hàm số y=f(x) xác định, liên tục trên và có bảng biến thiên như sau:
Giá trị lớn nhất của hàm số y=f(x) trên đoạn [ 0; 2] bằng:
-
Tìm GTLN và GTNN của hàm số \(f(x)=\left(x^{2}-2\right) \cdot e^{2 x}\) trên đoạn [-1 ; 2].
-
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên trên đoạn \(\left[ { – 1;4} \right]\) như sau:
.png)
Giá trị lớn nhất của hàm số \(y = \left| {f\left( x \right)} \right|\) trên đoạn đoạn \(\left[ { – 1;4} \right]\) bằng
-
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số\(g(x)=f\left(4 x-x^{2}\right)+\frac{1}{3} x^{3}-3 x^{2}+8 x+\frac{1}{3}\) trên đoạn [1;3]?
-
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{3x - 11}}{{x + 2}}\text{ trên đoạn } \left[ {1;5} \right]\)
-
Tìm giá trị nhỏ nhất m của hàm số \(y=x^{4}-x^{2}+13\) trên đoạn [-2;3].
-
Tìm GTLN của hàm số \(y = x - \sqrt {{x^2} + 1} \) ?
-
Xét hàm số \(y = \frac{{{x^2}}}{{x - 1}}\)
Trong các khẳng định sau, khẳng định nào là đúng?
-
Hàm số \(y=x+\frac{1}{x}+x^{2}+\frac{1}{x^{2}}\) có giá trị nhỏ nhất, giá trị lớn nhất trên đoạn [ 1; 3] là:
-
Giá trị nhỏ nhất của hàm số \(y=\frac{1}{\sin x}\)trên khoảng (0;π ) là:
-
Một nhà sản xuất cần thiết kế một thùng sơn dạng hình trụ có nắp đậy với dung tích 1000 cm3. Biết rằng bán kính của nắp đậy sao cho nhà sản xuất tiết kiệm nguyên vật liệu nhất có giá trị là a. Hỏi giá trị a gần với giá trị nào nhất dưới đây?
-
Hàm số \(y=\frac{x^{2}-2}{\sqrt{x^{2}+1}}\) có giá trị nhỏ nhất tại điểm có hoành độ bằng:
-
Cho hàm số \(y=\frac{x+1}{2x-1}\). Chọn phương án đúng trong các phương án sau
-
Hàm số \(y=\frac{\sin x+1}{\sin ^{2} x+3}\) đạt giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \(\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right]\) - tại điểm có hoành độ bằng
-
Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-x-1\right)\) trên đoạn [0;2] là
-
Xét hàm số \(\begin{equation} f(x)=\left|x^{2}+a x+b\right| \end{equation}\) , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số
trên [-1;3]. Khi M nhận giá trị nhỏ nhất tính \(\begin{equation} T=a+2 b \text { . } \end{equation}\) -
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = – 3 + \sqrt {4 – {x^2}} \) lần lượt là.
