Tuyển Tập Đề Thi Tham Khảo Tốt Nghiệp THPT Quốc Gia Năm 2025 - Toán - Bộ Đề 01 - Đề Số 03
Câu 1
Tính tích phân \(I=\int_{-1}^{0}{\left( 2x+1 \right)}dx\).
A.\(I=0\).
B.\(I=1\).
C.\(I=2\).
D.\(I=-\frac{1}{2}\).
Câu 2
Cho hàm số \(y=f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ a;b \right]\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a,x=b\) được tính theo công thức:
A.\(S=\int_{a}^{b}{\left| f\left( x \right) \right|}\text{d}x\).
B.\(S=\int_{a}^{b}{f}\left( x \right)\text{d}x\).
C.\(S=-\int_{a}^{b}{f}\left( x \right)\text{d}x\).
D.\(S=\int_{b}^{a}{\left| f\left( x \right) \right|}\text{d}x\).
Câu 3
Cho mẫu số liệu ghép nhóm có bảng tần số ghép nhóm như sau:
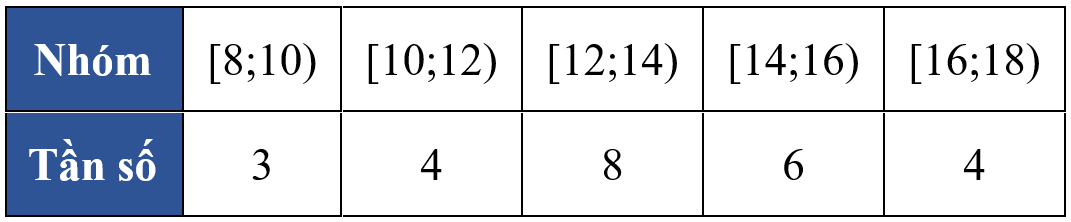
Trung vị của bảng số liệu trên thuộc nhóm nào?
A.\(\left[ 12;14 \right)\).
B.\(\left[ 10;12 \right)\).
C.\(\left[ 14;16 \right)\).
D.\(\left[ 16;18 \right)\).
Câu 4
Trong không gian \(Oxyz\), cho mặt phẳng
\(\left( P \right):2x+3y+z+2=0\).
Vectơ nào dưới đây là một véctơ pháp tuyến của \(\left( P \right)\)?
A.\({{\vec{n}}_{3}}\left( 2;3;2 \right)\).
B.\({{\vec{n}}_{1}}\left( 2;3;0 \right)\).
C.\({{\vec{n}}_{2}}\left( 2;3;1 \right)\).
D.\({{\vec{n}}_{4}}\left( 2;0;3 \right)\).
Câu 5
Tiệm cận ngang của đồ thị hàm số \(y=\frac{4x+1}{x-1}\) là:
A.\(y=\frac{1}{4}\).
B.\(y=4\).
C.\(y=1\).
D.\(y=-1\).
Câu 6
Nghiệm của phương trình \(\text{lo}{{\text{g}}_{3}}\left( x-1 \right)=2\) là:
A.\(x=8\).
B.\(x=9\).
C.\(x=7\).
D.\(x=10\).
Câu 7
Trong không gian \(Oxyz\), đường thẳng \(d:\left\{ \begin{array}{*{35}{l}} x=2-t \\ y=1+2t \\ z=3+t \\\end{array} \right.\) có một vectơ chỉ phương là:
A.\(\overrightarrow{{{u}_{1}}}=\left( -1;2;3 \right)\).
B.\(\overrightarrow{{{u}_{3}}}=\left( 2;1;3 \right)\).
C.\(\overrightarrow{{{u}_{4}}}=\left( -1;2;1 \right)\).
D.\(\overrightarrow{{{u}_{2}}}=\left( 2;1;1 \right)\).
Câu 8
Cho hai đường thẳng phân biệt \(a, b\) và mặt phẳng \(\left( P \right)\). Chọn khẳng định đúng?
A.Nếu \(a // \left( P \right)\) và \(b\bot a\) thì \(b\bot \left( P \right)\).
B.Nếu \(a // \left( P \right)\) và \(b\bot \left( P \right)\) thì \(b\bot a\).
C.Nếu \(a\bot \left( P \right)\) và \(b\bot a\) thì \(b // \left( P \right)\).
D.Nếu \(a // \left( P \right)\) và \(b // \left( P \right)\) thì \(b // a\).
Câu 9
Tập nghiệm của bất phương trình \({{2}^{2x}}<{{2}^{x+6}}\) là:
A.\(\left( -\infty ;6 \right)\).
B.\(\left( 0;64 \right)\).
C.\(\left( 6;+\infty \right)\).
D.\(\left( 0;6 \right)\)
Câu 10
Dãy số nào sau đây là cấp số cộng?
A.\(\left( {{u}_{n}} \right):{{u}_{n}}=\frac{1}{n}\).
B.\(\left( {{u}_{n}} \right):{{u}_{n}}={{u}_{n-1}}-2,\forall n\ge 2\).
C.\(\left( {{u}_{n}} \right):{{u}_{n}}={{2}^{n}}-1\).
D.\(\left( {{u}_{n}} \right):{{u}_{n}}=2{{u}_{n-1}},\forall n\ge 2\).
Câu 11
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\). Mệnh đề nào sau đây sai?
A.\(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}'}=\overrightarrow{A{C}'}\).
B.\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\).
C.\(\left| \overrightarrow{AB}\left| = \right|\overrightarrow{CD} \right|\).
D.\(\overrightarrow{AB}=\overrightarrow{CD}\).
Câu 12
Cho hàm số \(y=f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.\(\left( -\infty ;-1 \right)\).
B.\(\left( -1;1 \right)\).
C.\(\left( 0;+\infty \right)\).
D.\(\left( -\infty ;+\infty \right)\).
Câu 13
Cho hàm số \(y=-{{x}^{3}}-3{{x}^{2}}-9x+3\) có đạo hàm trên \(\mathbb{R}\).
a) Hàm số có ba điểm cực trị.
b) Hàm số nghịch biến trên tập xác định của nó.
c) \(\underset{x\in \left( -4;4 \right]}{\mathop{\text{Min}}}\,f\left( x \right)=f\left( 4 \right)\).
d) Đồ thị hàm số \(y=-{{x}^{3}}-3{{x}^{2}}-9x+3\) cắt trục hoành tại 1 điểm duy nhất.
Câu 14
Sau khi xuất phát, ô tô di chuyển với tốc độ
\(v\left( t \right)=2,01t-0,025{{t}^{2}}\left( 0\le t\le 10 \right)\).
Trong đó \(v\left( t \right)\) tính theo \(\text{m}/\text{s}\), thời gian \(t\) tính theo \(s\) với \(t=0\) là thời điểm xe xuất phát.
a) Quãng đường xe di chuyển được tính theo công thức là:
\(s\left( t \right)=2,01-0,05t\left( 0\le t\le 10 \right)\).
b) Quãng đường xe di chuyển được trong \(3\left( s \right)\) kể từ khi bắt đầu là \(8,82\left( \text{m} \right)\).
c) Quãng đường xe di chuyển được trong giây thứ 3 xấp xỉ 4,867(m).
d) Trong khoảng thời gian không quá 10 s đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe là \(1,51\text{ }\!\!~\!\!\text{ m}/{{\text{s}}^{2}}\).
Câu 15
Một công ty thiết bị Giáo Dục đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là \(50\text{ }\!\!%\!\!\text{ }\) và dự án 2 là \(60\text{ }\!\!%\!\!\text{ }\). Khả năng thắng thầu cả 2 dự án là \(30\text{ }\!\!%\!\!\text{ }\). Gọi \(\text{A},\text{B}\) lần lượt là biến cố thắng thầu dự án 1 và dự án 2.
a) A và B là hai biến độc lập.
b) Xác suất công ty thắng thầu đúng 1 dự án là \(50\text{ }\!\!%\!\!\text{ }\).
c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là \(60\text{ }\!\!%\!\!\text{ }\).
d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là \(60\text{ }\!\!%\!\!\text{ }\).
Câu 16
Cho các điểm \(A\left( 1;-2;0 \right)\); \(B\left( 2;-1;1 \right)\); \(C\left( 1;1;2 \right)\).
a) Phương trình mặt phẳng \(\left( ABC \right)\) là
\(x+2y-3z-3=0\).b) Phương trình mặt phẳng \(\left( \alpha \right)\) qua \(A\) và vuông góc với \(BC\) là:
\(x-2y-z-5=0\).
c) Phương trình mặt phẳng trung trực \(\left( \beta \right)\) của đoạn \(AC\) là:
\(6y+4z-1=0\).
d) Phương trình mặt phẳng \(\left( \gamma \right)\) chứa trục \(Ox\) và điểm \(C\) là:
\(2y+z=0\).
Top 10/0 lượt thi
| Tên | Điểm | Thời gian |
|---|















