ADMICRO
Giá trị nhỏ nhất của hàm số \(y = \dfrac{1}{4}{x^4} - \dfrac{{27}}{2}{x^2} + 3\) trên đoạn \(\left[ {0;80} \right]\) bằng?
Chính xác
Xem lời giải
Hãy suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ADSENSE / 4
Chủ đề: Đề thi Học Kỳ/Giữa Kỳ
Môn: Toán Lớp 12
Lời giải:
Báo saiTXĐ: \(D = \mathbb{R}\).
Xét hàm số \(y = \dfrac{1}{4}{x^4} - \dfrac{{27}}{2}{x^2} + 3\) trên \(\left[ {0;80} \right]\) ta có:
\(y' = {x^3} - 27x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 3\sqrt 3 }\\{x = {\rm{\;}} - 3\sqrt 3 }\end{array}} \right.\)
Bảng biến thiên trên đoạn \(\left[ {0;80} \right]\):
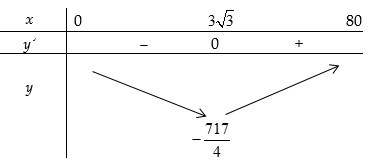
Dựa vào bảng biến thiên ta thấy \(\mathop {\min }\limits_{\left[ {0;80} \right]} y = y\left( {3\sqrt 3 } \right) = {\rm{ \;}} - \dfrac{{717}}{4}\).
Chọn C.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi giữa HK1 môn Toán 12 năm 2023-2024
Trường THPT Trần Hữu Trang
02/12/2024
135 lượt thi
0/40
Bắt đầu thi
ZUNIA12
ZUNIA9
AANETWORK