10 Đề thi kiểm tra cuối HK1 môn Toán lớp 8 - Cánh Diều - Đề 5

Cho các biểu thức: \({{x}^{2}}+{{y}^{2}};2025;\frac{3}{x}+y;\frac{x}{y}+\frac{1}{5}x;\frac{x}{2}+xyz;4+x\sqrt{yz}\) có bao nhiêu đa thức?

Biểu thức \({{(x+2)}^{3}}-{{(x-2)}^{3}}\) được rút gọn thành:

Phân thức nào sau đây có tử thức là \(2x-1\) và mẫu thức là \({{x}^{2}}-1\) ?

Đa thức nào sau đây không là mẫu thức chung của hai phân thức \(\frac{1}{x};\frac{1}{{{y}^{2}}}\) ?

Cho hàm số \(y=f\left( x \right)=2{{x}^{2}}-1\). Khẳng định nào sau đây là đúng?

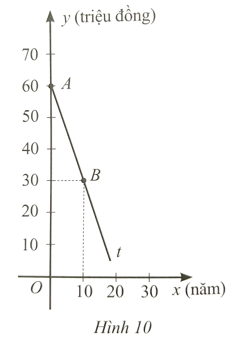
Cho điểm \(A\) và \(B\) trong mặt phẳng tọa độ Oxy như hình bên. Khẳng định nào sau đây là đúng?

Giá trị của \(m\) để đồ thị hàm số \(y=\left( m+2 \right)x+5\) là đường thẳng có hệ số góc bằng -3 là

Cho \(\left( {{d}_{m}} \right):y=mx+2\). Kết luận nào sau đây là đúng?

Hình chóp nào sau đây là hình chóp tứ giác đều?

Một hình chóp đều có nửa chu vi đáy \(p\) và độ dài trung đoạn \(d\) thì diện tích xung quanh \({{S}_{xq}}\) của hình chóp đều đó là

Tứ giác \(ABCD\) có số đo các góc \(\widehat{A},\widehat{B},\widehat{C},\widehat{D}\) tỉ lệ thuận với \(4;3;5;6\). Khi đó số đo \(\widehat{A}\) là

Chọn nhận định sai.

Tứ giác nào có hai đường chéo bằng nhau?

Cho biểu thức: \(P=\left( \frac{1}{x-1}-\frac{x}{1-{{x}^{3}}}\cdot \frac{{{x}^{2}}+x+1}{x+1} \right):\frac{2x+1}{{{x}^{2}}+2x+1}\).

Tính giá trị của \(P\) khi \(x=\frac{1}{2}\)

Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao \(k\) (triệu đồng) với \(0<k<60\). Gọi \(y\) (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau \(x\) năm sử dụng.

Trong hình vẽ trên, tia At là một phần của đường thẳng \(y=ax+b\). Tìm a, Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu

Cho ba số \(a,b,c\) đôi một khác nhau và thỏa mãn: \({{(a+b+c)}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}.\)

Tính giá trị biểu thức \(T=\frac{{{a}^{3}}{{b}^{3}}+{{b}^{3}}{{c}^{3}}+{{c}^{3}}{{a}^{3}}}{3{{a}^{2}}{{b}^{2}}{{c}^{2}}}+\left( 1+\frac{a}{c} \right)\left( 1+\frac{b}{a} \right)\left( 1+\frac{c}{b} \right)\)